From transistor to trapped-ion computers for quantum chemistry
- PMID: 24395054
- PMCID: PMC5378044
- DOI: 10.1038/srep03589
From transistor to trapped-ion computers for quantum chemistry
Abstract
Over the last few decades, quantum chemistry has progressed through the development of computational methods based on modern digital computers. However, these methods can hardly fulfill the exponentially-growing resource requirements when applied to large quantum systems. As pointed out by Feynman, this restriction is intrinsic to all computational models based on classical physics. Recently, the rapid advancement of trapped-ion technologies has opened new possibilities for quantum control and quantum simulations. Here, we present an efficient toolkit that exploits both the internal and motional degrees of freedom of trapped ions for solving problems in quantum chemistry, including molecular electronic structure, molecular dynamics, and vibronic coupling. We focus on applications that go beyond the capacity of classical computers, but may be realizable on state-of-the-art trapped-ion systems. These results allow us to envision a new paradigm of quantum chemistry that shifts from the current transistor to a near-future trapped-ion-based technology.
Conflict of interest statement
The authors declare no competing financial interests.
Figures

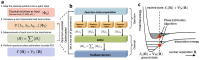

 (a),
(a),  (b) and
(b) and  (c). The initial state considered is |↑↑↓↓〉, in the qubit representation of the Hartree-Fock state in a molecular orbital basis with one electron on the first and second orbital. Vertical lines and arrows define the time domain in which the dominant part of the error is due to the digital approximation. d) Energy of the system, in h11 units, for the initial state | ↑↑↓↓〉 for the exact dynamics, versus the digitized one. For a protocol with three Trotter steps the energy is recovered up to a negligible error.
(c). The initial state considered is |↑↑↓↓〉, in the qubit representation of the Hartree-Fock state in a molecular orbital basis with one electron on the first and second orbital. Vertical lines and arrows define the time domain in which the dominant part of the error is due to the digital approximation. d) Energy of the system, in h11 units, for the initial state | ↑↑↓↓〉 for the exact dynamics, versus the digitized one. For a protocol with three Trotter steps the energy is recovered up to a negligible error.References
-
- Dirac P. A. M. Quantum Mechanics of Many-Electron Systems. Proc. R. Soc. A 123, 714–733 (1929).
-
- Love P. J. Back to the Future: A roadmap for quantum simulation from vintage quantum chemistry. eprint arXiv:1208.5524. (2012). (To Appear in Advances in Chemical Physics).
-
- Head-Gordon M. & Artacho E. Chemistry on the computer. Phys. Today , 61, 58 (2008).
-
- Feynman R. P. Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488 (1982).
-
- Kassal I., Whitfield J. D., Perdomo-Ortiz A., Yung M.-H. & Aspuru-Guzik A. Simulating chemistry using quantum computers. Annu. Rev. Phys. Chem. 62, 185207 (2011). - PubMed
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

