Simultaneous identification of growth law and estimation of its rate parameter for biological growth data: a new approach

Abstract

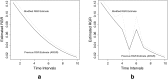
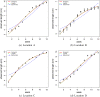
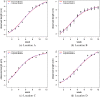
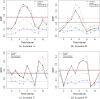
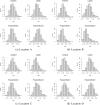
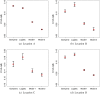
Scientific formalizations of the notion of growth and measurement of the rate of growth in living organisms are age-old problems. The most frequently used metric, "Average Relative Growth Rate" is invariant under the choice of the underlying growth model. Theoretically, the estimated rate parameter and relative growth rate remain constant for all mutually exclusive and exhaustive time intervals if the underlying law is exponential but not for other common growth laws (e.g., logistic, Gompertz, power, general logistic). We propose a new growth metric specific to a particular growth law and show that it is capable of identifying the underlying growth model. The metric remains constant over different time intervals if the underlying law is true, while the extent of its variation reflects the departure of the assumed model from the true one. We propose a new estimator of the relative growth rate, which is more sensitive to the true underlying model than the existing one. The advantage of using this is that it can detect crucial intervals where the growth process is erratic and unusual. It may help experimental scientists to study more closely the effect of the parameters responsible for the growth of the organism/population under study.

Fig. 1

Departure of ISRP from ORP under Logistic and Gompertz growth laws. The figure (a) demonstrates that, if the data is simulated using logistic growth model, then the values of ISRP computed from logistic model will be constant over time. However, ISRP computed from other growth law eg. Gompertz or Exponential will not be constant. Similar result holds true for data if simulated using Gompertz growth model (figure (b))

Fig. 2

The graph of a modified estimate of RGR when the underlying simulated model is known to be logistic (dotted line). The dotted line represents the estimate of RGR assuming exponential growth between two consecutive time intervals (a). (b): If the true model is contaminated by replacing only one observation 5.435020, at the 6th time point by 5.4, then modified estimates are shown. It is to be noted that, the modified estimates of RGR have some bias and that these are more sensitive to the departure of data from the true model. a Modified RGR estimate with logistic growth (15) as true model (dotted line). Estimate of ARGR (solid line). b Sensitivity of RGR estimates if a data point is replaced with a small error

Fig. 3

All three models Gompertz, Logistic and Exponential growth are fitted to the data obtained from four locations A, B, C and D. Red, green and blue colors denote the fit of Gompertz, logistic and exponential models respectively. The estimate details of parameters are provided in Table 2

Fig. 4

Proposed models (17) and (18) are fitted to the data from locations A, B, C and D. The red and blue lines denote the fit of models (17) and (18) respectively

Fig. 5

The four models Gompertz, Logistic, Proposed models (17) and (18) are compared with respect to ISRP to the data obtained from four locations A, B, C and D. Black, red, green and blue colors denote the fit of Gompertz, logistic, models (17) and (18) respectively (see text for discussion)

Fig. 6

The bootstrap distribution of σ(d) for each of the growth models for all locations A, B, C and D based on 1000 bootstrap replications. From the bootstrap distributions of the deviations of ISRP from the constant rate parameter it is clear that proposed model 2 ISRP is closest to the corresponding rate parameter b

Fig. 7

Bootstrap confidence intervals of the population mean of σ(d) for locations A, B, C and D for the four growth models. It is clear that the proposed model 2 has the lowest mean value of σ(d) for all locations

Fig. 8

Absolute error affecting the ISRP for (a) exponential, (b) linear and (c) Gompertz growth laws with respect to relative errors α and β