The Gaussian shear wave in a dispersive medium

Abstract

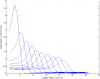
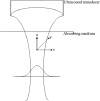
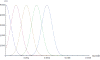
In "imaging the biomechanical properties of tissues," a number of approaches analyze shear wave propagation initiated by a short radiation force push. Unfortunately, it has been experimentally observed that the displacement-versus-time curves for lossy tissues are rapidly damped and distorted in ways that can confound simple tracking approaches. This article addresses the propagation, decay and distortion of pulses in lossy and dispersive media, to derive closed-form analytic expressions for the propagating pulses. The theory identifies key terms that drive the distortion and broadening of the pulse. Furthermore, the approach taken is not dependent on any particular viscoelastic model of tissue, but instead takes a general first-order approach to dispersion. Examples with a Gaussian beam pattern and realistic dispersion parameters are given along with general guidelines for identifying the features of the distorting wave that are the most compact.

Keywords: Attenuation; Dispersion; Distortion; Propagation; Radiation force; Shear wave.

Figure 1

Experimental data demonstrating the displacements (vertical axis) in a gelatin phantom at different radial positions (horizontal axis) at 1, 2, 3…msec time intervals, following a short radiation force pulse at 5 MHz. The displacements were calculated from tracking scans taken after the radiation force push. An approximately Gaussian, axially symmetric beam pattern was produced at the focal depth with a standard deviation of approx. 1 mm. In a low-loss, low dispersion media such as gelatin, the amplitude loss is largely due to cylindrical spreading. Still, the long tail of the displacement curves and softening of the leading edge can be seen. Decay and distortion of the propagating wave are more pronounced in lossy tissues.

Figure 2

Schematic of a Gaussian beam, high f number, applied in an absorbing medium to produce a radiation force push.

Figure 3

The comparison of a Gaussian function of σ = 2 units and a substitute function $\frac{1}{{(r^2+1)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}$, both normalized to unit amplitude at r = 0. The substitute function and its Hankel transform lead to an analytical solution which is useful for illustrating the effects of dispersion. However, it has a slow asymptotic decay of $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$r$}\right.$, and therefore much wider “tails” compared with the Gaussian.

Figure 4

Theoretical values of velocity (arbitrary units) vs. time (sec.) profiles for the right-traveling shear wave of the one dimensional case, at observation points 0, 2, 4, 6, and 8 mm from the center of the Gaussian beam. In 4a is the simple case of the lossless medium, reducing to D'Alembert's solution. In 4b is the same initial beam and observation points but with modest loss and dispersion characteristic of some soft tissues.

Figure 4

Theoretical values of velocity (arbitrary units) vs. time (sec.) profiles for the right-traveling shear wave of the one dimensional case, at observation points 0, 2, 4, 6, and 8 mm from the center of the Gaussian beam. In 4a is the simple case of the lossless medium, reducing to D'Alembert's solution. In 4b is the same initial beam and observation points but with modest loss and dispersion characteristic of some soft tissues.

Figure 5

Theoretical values of velocity (arbitrary units) vs. time (sec.) profiles for the shear wave of the cylindrical case, at observation points 0, 2, 4, 6, and 8 mm radially from the center of an approximately Gaussian beam. Rapid initial loss of amplitude followed by cylindrical spreading is seen even in the lossless case, Figure 5a. With dispersion, Figure 5b, the smoothing of the waveforms and amplitude losses are pronounced.

Figure 5

Theoretical values of velocity (arbitrary units) vs. time (sec.) profiles for the shear wave of the cylindrical case, at observation points 0, 2, 4, 6, and 8 mm radially from the center of an approximately Gaussian beam. Rapid initial loss of amplitude followed by cylindrical spreading is seen even in the lossless case, Figure 5a. With dispersion, Figure 5b, the smoothing of the waveforms and amplitude losses are pronounced.