Mean-field models for heterogeneous networks of two-dimensional integrate and fire neurons
- PMID: 24416013
- PMCID: PMC3873638
- DOI: 10.3389/fncom.2013.00184
Mean-field models for heterogeneous networks of two-dimensional integrate and fire neurons
Abstract
We analytically derive mean-field models for all-to-all coupled networks of heterogeneous, adapting, two-dimensional integrate and fire neurons. The class of models we consider includes the Izhikevich, adaptive exponential and quartic integrate and fire models. The heterogeneity in the parameters leads to different moment closure assumptions that can be made in the derivation of the mean-field model from the population density equation for the large network. Three different moment closure assumptions lead to three different mean-field systems. These systems can be used for distinct purposes such as bifurcation analysis of the large networks, prediction of steady state firing rate distributions, parameter estimation for actual neurons and faster exploration of the parameter space. We use the mean-field systems to analyze adaptation induced bursting under realistic sources of heterogeneity in multiple parameters. Our analysis demonstrates that the presence of heterogeneity causes the Hopf bifurcation associated with the emergence of bursting to change from sub-critical to super-critical. This is confirmed with numerical simulations of the full network for biologically reasonable parameter values. This change decreases the plausibility of adaptation being the cause of bursting in hippocampal area CA3, an area with a sizable population of heavily coupled, strongly adapting neurons.
Keywords: bifurcation analysis; bursting; hippocampus; integrate-and-fire neuron; mean-field model.
Figures
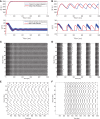
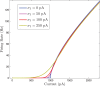
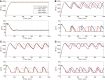
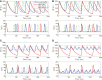
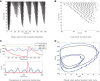

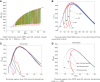
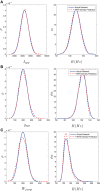
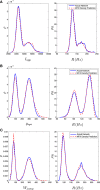
Similar articles
-
Exact mean-field models for spiking neural networks with adaptation.J Comput Neurosci. 2022 Nov;50(4):445-469. doi: 10.1007/s10827-022-00825-9. Epub 2022 Jul 14. J Comput Neurosci. 2022. PMID: 35834100
-
Bifurcations of large networks of two-dimensional integrate and fire neurons.J Comput Neurosci. 2013 Aug;35(1):87-108. doi: 10.1007/s10827-013-0442-z. Epub 2013 Feb 21. J Comput Neurosci. 2013. PMID: 23430291
-
Firing patterns in the adaptive exponential integrate-and-fire model.Biol Cybern. 2008 Nov;99(4-5):335-47. doi: 10.1007/s00422-008-0264-7. Epub 2008 Nov 15. Biol Cybern. 2008. PMID: 19011922 Free PMC article.
-
Low-dimensional spike rate models derived from networks of adaptive integrate-and-fire neurons: Comparison and implementation.PLoS Comput Biol. 2017 Jun 23;13(6):e1005545. doi: 10.1371/journal.pcbi.1005545. eCollection 2017 Jun. PLoS Comput Biol. 2017. PMID: 28644841 Free PMC article.
-
Statistical physics approaches to neuronal network dynamics.Sheng Li Xue Bao. 2011 Oct 25;63(5):453-62. Sheng Li Xue Bao. 2011. PMID: 22002236 Review.
Cited by
-
Differential effects of excitatory and inhibitory heterogeneity on the gain and asynchronous state of sparse cortical networks.Front Comput Neurosci. 2014 Sep 12;8:107. doi: 10.3389/fncom.2014.00107. eCollection 2014. Front Comput Neurosci. 2014. PMID: 25309409 Free PMC article.
-
Simple, biologically-constrained CA1 pyramidal cell models using an intact, whole hippocampus context.F1000Res. 2014 May 9;3:104. doi: 10.12688/f1000research.3894.1. eCollection 2014. F1000Res. 2014. PMID: 25383182 Free PMC article.
-
Interaction between synaptic inhibition and glial-potassium dynamics leads to diverse seizure transition modes in biophysical models of human focal seizures.J Comput Neurosci. 2016 Oct;41(2):225-44. doi: 10.1007/s10827-016-0615-7. Epub 2016 Aug 3. J Comput Neurosci. 2016. PMID: 27488433 Free PMC article.
-
From neuronal populations to behavior: a computational journey.Front Comput Neurosci. 2014 Aug 1;8:81. doi: 10.3389/fncom.2014.00081. eCollection 2014. Front Comput Neurosci. 2014. PMID: 25136313 Free PMC article. No abstract available.
-
Analytical approximations of the firing rate of an adaptive exponential integrate-and-fire neuron in the presence of synaptic noise.Front Comput Neurosci. 2014 Sep 18;8:116. doi: 10.3389/fncom.2014.00116. eCollection 2014. Front Comput Neurosci. 2014. PMID: 25278872 Free PMC article.
References
-
- Abbott L. F., van Vreeswijk C. (1993). Asynchronous states in networks of pulse-coupled oscillators. Learn Mem. 48, 1483–1490 - PubMed
-
- Andersen P., Morris R., Amaral D., Bliss T., O'Keefe J. (eds.). (2006). The Hippocampus Book. Oxford: Oxford University Press
LinkOut - more resources
Full Text Sources
Other Literature Sources
Miscellaneous

