Identifying optimal models to represent biochemical systems
- PMID: 24416170
- PMCID: PMC3885518
- DOI: 10.1371/journal.pone.0083664
Identifying optimal models to represent biochemical systems
Abstract
Biochemical systems involving a high number of components with intricate interactions often lead to complex models containing a large number of parameters. Although a large model could describe in detail the mechanisms that underlie the system, its very large size may hinder us in understanding the key elements of the system. Also in terms of parameter identification, large models are often problematic. Therefore, a reduced model may be preferred to represent the system. Yet, in order to efficaciously replace the large model, the reduced model should have the same ability as the large model to produce reliable predictions for a broad set of testable experimental conditions. We present a novel method to extract an "optimal" reduced model from a large model to represent biochemical systems by combining a reduction method and a model discrimination method. The former assures that the reduced model contains only those components that are important to produce the dynamics observed in given experiments, whereas the latter ensures that the reduced model gives a good prediction for any feasible experimental conditions that are relevant to answer questions at hand. These two techniques are applied iteratively. The method reveals the biological core of a model mathematically, indicating the processes that are likely to be responsible for certain behavior. We demonstrate the algorithm on two realistic model examples. We show that in both cases the core is substantially smaller than the full model.
Conflict of interest statement
Figures
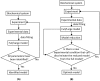
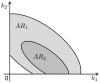
 . In this situation, a reduced model can be obtained either by setting
. In this situation, a reduced model can be obtained either by setting  or
or  . When a new dataset from a new experiment is incorporated, the admissible region shrinks to
. When a new dataset from a new experiment is incorporated, the admissible region shrinks to  . Thus,
. Thus,  . Now, a reduced model can only be obtained when
. Now, a reduced model can only be obtained when  .
.

 as well as by the reduced model with
as well as by the reduced model with  .
.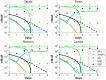
 from the full model with
from the full model with  . When an experiment is conducted for this mutant, we obtain the dataset that is denoted by ‘*’.
. When an experiment is conducted for this mutant, we obtain the dataset that is denoted by ‘*’.
 in (22).
in (22).
 as well as by the reduced model with
as well as by the reduced model with  .
.
 ,
,  , and
, and  respectively. Predictions from the optimal model are indicated by the dashed lines.
respectively. Predictions from the optimal model are indicated by the dashed lines.References
-
- Roussel MR, Fraser SJ (2001) Invariant manifold methods for metabolic model reduction. Chaos 11: 196–206. - PubMed
-
- Kooi BW, Poggiale JC, Auger P, Kooijman SALM (2002) Aggregation methods in food chains with nutrient recycling. Ecological Modelling 157: 69–86.
-
- Surovtsova I, Simus N, Lorenz T, Konig A, Sahle S, et al. (2009) Accessible methods for the dynamic time-scale decomposition of biochemical systems. Bioinformatics 25: 2816–2823. - PubMed
-
- Turányi T (1990) Sensitivity analysis of complex kinetic systems. tools and applications. Journal of Mathematical Chemistry 5: 203–248.
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

