Dynamics between cancer cell subpopulations reveals a model coordinating with both hierarchical and stochastic concepts

Abstract

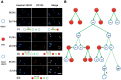
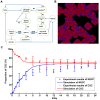
Tumors are often heterogeneous in which tumor cells of different phenotypes have distinct properties. For scientific and clinical interests, it is of fundamental importance to understand their properties and the dynamic variations among different phenotypes, specifically under radio- and/or chemo-therapy. Currently there are two controversial models describing tumor heterogeneity, the cancer stem cell (CSC) model and the stochastic model. To clarify the controversy, we measured probabilities of different division types and transitions of cells via in situ immunofluorescence. Based on the experiment data, we constructed a model that combines the CSC with the stochastic concepts, showing the existence of both distinctive CSC subpopulations and the stochastic transitions from NSCCs to CSCs. The results showed that the dynamic variations between CSCs and non-stem cancer cells (NSCCs) can be simulated with the model. Further studies also showed that the model can be used to describe the dynamics of the two subpopulations after radiation treatment. More importantly, analysis demonstrated that the experimental detectable equilibrium CSC proportion can be achieved only when the stochastic transitions from NSCCs to CSCs occur, indicating that tumor heterogeneity may exist in a model coordinating with both the CSC and the stochastic concepts. The mathematic model based on experimental parameters may contribute to a better understanding of the tumor heterogeneity, and provide references on the dynamics of CSC subpopulation during radiotherapy.

Figure 1. Divisions and transitions of CSCs/NSCCs as well as kinetics and scheme of the model.

(A). Typical division types of CSCs/NSCCs and transition from NSCC to CSC. Scale bar equals 50 µm. (a–b) Typical in situ division type of a NSCC (white arrow) and transition from a NSCC to a CSC (yellow arrow); (c–d). Typical in situ symmetric divisions of CSCs: self-renewal (one CSC divides into two CSCs) and differentiation (One CSC divides into two NSCCs); NSCC (white arrow), CSC (yellow arrow). (e–f). Typical in situ asymmetric division of CSC (One CSC divide into one CSC and one NSCC); NSCC (white arrow), CSC (yellow arrow). (i). Kinetic equations that correspond to the phenomena in a and b. (ii) Kinetic equations that correspond to the phenomena in c and d. (iii)Kinetic equation that corresponds to the phenomenon in e and f. (B). Scheme of the model based on the experimental results.

Figure 2. Experiments procedures, results and the simulations of long-term dynamics between CSC and NSCC subpopulations.

(A). Diagram of experiment procedures; (B). Comparison between simulation results and experiment results; (C). Experimental results of long-term equilibrium CSC proportions from initial purified CSCs and NSCCs.

Figure 3. The long-term dynamics between CSC and NSCC subpopulations via cellular automaton simulation method.

(A). Calculation scheme for cellular automaton method. (B). Typical result of simulation with cellular automaton method (initial condition is that all the cells are NSCCs). Red: CSC; Blue: NSCC; Black: vacant lattice. (C). Comparison between simulation results with cellular automaton method and experimental results.

Figure 4. Radiation experiments procedures and simulations of long-term dynamics between CSC and NSCC subpopulations.

(A). Diagram of experiment procedures with radiation treatment; (B). Comparison between simulation and experiment results in 0–24 day (radiation is applied when t is 0 day); (C). Amplified image of the results from irradiated 70% CSC group (0–2d) (radiation is applied when t is 0 day).

Figure 5. Impact on the long-term dynamics between CSC and NSCC subpopulations with sorting error.

(A). Diagram of sorting error in the experiments; (B). Comparison between simulation (K_T = 0) and experiment results.