Stability switches and double Hopf bifurcation in a two-neural network system with multiple delays

Abstract

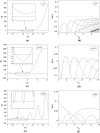
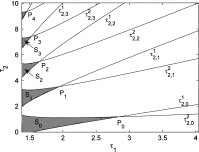
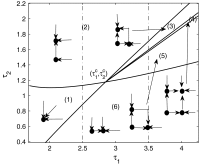
Time delay is an inevitable factor in neural networks due to the finite propagation velocity and switching speed. Neural system may lose its stability even for very small delay. In this paper, a two-neural network system with the different types of delays involved in self- and neighbor- connection has been investigated. The local asymptotic stability of the equilibrium point is studied by analyzing the corresponding characteristic equation. It is found that the multiple delays can lead the system dynamic behavior to exhibit stability switches. The delay-dependent stability regions are illustrated in the delay-parameter plane, followed which the double Hopf bifurcation points can be obtained from the intersection points of the first and second Hopf bifurcation, i.e., the corresponding characteristic equation has two pairs of imaginary eigenvalues. Taking the delays as the bifurcation parameters, the classification and bifurcation sets are obtained in terms of the central manifold reduction and normal form method. The dynamical behavior of system may exhibit the quasi-periodic solutions due to the Neimark- Sacker bifurcation. Finally, numerical simulations are made to verify the theoretical results.

Keywords: Double Hopf bifurcation; Multiple delays; Neural network; Quasi-periodic behavior; Stability switches.

Fig. 1

Roofs of function G (left column) and eigenvalue real parts with τ ₂ varying (right column) for the fixed self-connection delay a–b , c–d and e–f , respectively. The other parameters are chosen as a ₁ = −6, a ₂ = 2.5, a ₃ = 2.5, a ₄ = −6, P = 0.4, Q = 0.4

Fig. 2

Distribution of eigenvalues with time delay τ ₂ varying a , b , c and d for the fixed parameters a ₁ = −6, a ₂ = 2.5, a ₃ = 2.5, a ₄ = −6, P = 0.4, Q = 0.4, , where the asterisk in green represents the eigenvalues with negative real part and one with positive real part is in red color

Fig. 3

Phase portraits with time delay τ ₂ varying a , b , c and d for the fixed parameters a ₁ = −6, a ₂ = 2.5, a ₃ = 2.5, a ₄ = −6, P = 0.4, Q = 0.4,

Fig. 4

Variation of the critical delay values τ ₂ with τ ₁ in the (τ ₁, τ ₂) parameter plane for the fixed parameters as a ₁ = −6, a ₂ = 2.5, a ₃ = 2.5, a ₄ = −6, P = 0.4 and Q = 0.4, respectively, where denote the stability regions of equilibrium point (x ₀, y ₀) and P_j, j = 0, 1, 2, … are the double Hopf bifurcation points

Fig. 5

a Roots of the characteristic equation in the complex plane for and b enlargement near (0, 0) corresponding to a, where the other parameters are fixed as a ₁ = −6, a ₂ = 2.5, a ₃ = 2.5, a ₄ = −6, P = 0.4, Q = 0.4

Fig. 6

Classification and bifurcation sets for system (1) near the first order point of the double Hopf bifurcations in the parameter (τ ₁, τ ₂) plane. The other parameters are chosen at the same as those in Fig. 4

Fig. 7

One-parameter bifurcation diagram with varying the delay τ ₂ for a τ ₁ = 2.5, τ ₂ ∈ [0.7,1], b τ ₁ = 2.5, τ ₂ ∈ [1.05, 1.3], c τ ₁ = 3.5, τ ₂ ∈ [1.1, 1.8], and d the partial enlargement of the c box, respectively. The other parameters are chosen at the same as those in Fig. 4

Fig. 8

Phase portraits of the numerical simulation for the dynamical behavior in system (1) near the first order point of the double Hopf bifurcation, where (τ ₁, τ ₂) is fixed as a (2.0, 0.8), b (2.5, 1.6), c (3.5, 1.6), d (3.5, 1.64), e (3.5, 1.4), and f (3.5, 0.8), respectively. The other parameters are chosen at the same as those in Fig. 4