Exploring accurate Poisson-Boltzmann methods for biomolecular simulations

Abstract

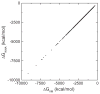
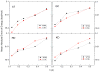
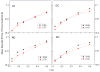
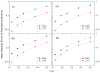
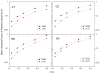
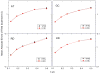
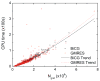
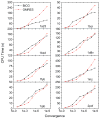
Accurate and efficient treatment of electrostatics is a crucial step in computational analyses of biomolecular structures and dynamics. In this study, we have explored a second-order finite-difference numerical method to solve the widely used Poisson-Boltzmann equation for electrostatic analyses of realistic bio-molecules. The so-called immersed interface method was first validated and found to be consistent with the classical weighted harmonic averaging method for a diversified set of test biomolecules. The numerical accuracy and convergence behaviors of the new method were next analyzed in its computation of numerical reaction field grid potentials, energies, and atomic solvation forces. Overall similar convergence behaviors were observed as those by the classical method. Interestingly, the new method was found to deliver more accurate and better-converged grid potentials than the classical method on or nearby the molecular surface, though the numerical advantage of the new method is reduced when grid potentials are extrapolated to the molecular surface. Our exploratory study indicates the need for further improving interpolation/extrapolation schemes in addition to the developments of higher-order numerical methods that have attracted most attention in the field.

Keywords: Continuum solvent models; Finite difference method; Immersed interface method; Poisson-Boltzmann equation.

Fig. 1

Correlation of reaction field energies (ΔG) by IIM and WHA at 1/2 Å grid spacing for the Amber training set of 579 biomolecules. The Pearson correlation coefficient is 1.0000 and the linear regression slope is 1.0014 (with fixed offset of zero).

Fig. 2

Mean absolute errors of reaction field potentials at the 8 nearest finite-difference grid points of each atom (kcal/mol-e) versus grid spacing h (Å) with respect to those calculated at the fine grid spacing of 1/16 Å for AT, GC, RD and KD dimers, respectively.

Fig. 3

Mean absolute errors of reaction field energies at each atom (kcal/mol) versus grid spacing h (Å) with respect to those calculated at the fine grid spacing of 1/16 Å for AT, GC, RD and KD dimers, respectively.

Fig. 4

Mean absolute errors of reaction field forces at each atom (kcal/mol-Å) versus grid spacing h (Å) with respect to those calculated at the fine grid spacing of 1/16 Å for AT, GC, RD and KD dimers, respectively.

Fig. 5

Mean absolute errors of reaction field potentials at the irregular grid points (inside, kcal/mol-e) versus grid spacing h (Å) with respect to those calculated at the fine grid spacing of 1/16 Å for AT, GC, RD and KD dimers, respectively.

Fig. 6

Mean absolute errors of potentials on the molecular surface (inside, kcal/mol-e) versus grid spacing h (Å) with respect to those calculated at the fine grid spacing of 1/16 Å for AT, GC, RD and KD dimers, respectively. A second-order least square fitting method was used in all tests.

Fig. 7

Mean absolute errors of reaction fields on the molecular surface (inside, kcal/mol-e-Å) versus grid spacing h (Å) with respect to those calculated at the fine grid spacing of 1/16 Å for AT, GC, RD and KD dimers, respectively. A second-order least square fitting method was used in all tests.

Fig. 8

CPU time versus the number of grids (N_grid) for GMRES and BiCG, respectively. Convergence criterion (relative) is set to be 10⁻⁶.

Fig. 9

CPU time versus convergence criterion for GMRES and BiCG, respectively, for the eight proteins listed in Table 1.