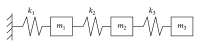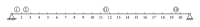Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2013 Dec 19:2013:235820.
doi: 10.1155/2013/235820. eCollection 2013.

A universal fast algorithm for sensitivity-based structural damage detection

Q W Yang  1 , J K Liu  2 , C H Li  1 , C F Liang  1
Affiliations

A universal fast algorithm for sensitivity-based structural damage detection

Q W Yang et al. ScientificWorldJournal. .

Abstract

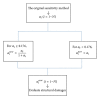
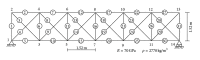
Structural damage detection using measured response data has emerged as a new research area in civil, mechanical, and aerospace engineering communities in recent years. In this paper, a universal fast algorithm is presented for sensitivity-based structural damage detection, which can quickly improve the calculation accuracy of the existing sensitivity-based technique without any high-order sensitivity analysis or multi-iterations. The key formula of the universal fast algorithm is derived from the stiffness and flexibility matrix spectral decomposition theory. With the introduction of the key formula, the proposed method is able to quickly achieve more accurate results than that obtained by the original sensitivity-based methods, regardless of whether the damage is small or large. Three examples are used to demonstrate the feasibility and superiority of the proposed method. It has been shown that the universal fast algorithm is simple to implement and quickly gains higher accuracy over the existing sensitivity-based damage detection methods.

PubMed Disclaimer

Figures

Figure 1
Figure 1
A graphical illustration of the universal fast algorithm.
Figure 2
Figure 2
Spring-mass system (Example 1).
Figure 3
Figure 3
Thirty-one-bar truss structure (Example 2).
Figure 4
Figure 4
A simple supported beam (Example 3).
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Chen J-C, Carba JA. On-orbit damage assessment for large space structures. AIAA Journal. 1988;26(9):1119–1126.
    1. Zimmerman DC, Kaouk M. Structural damage detection using a minimum rank update theory. Journal of Vibration and Acoustics. 1994;116(2):222–231.
    1. Doebling SW. Minimum-rank optimal update of elemental stiffness parameters for structural damage identification. AIAA Journal. 1996;34(12):2615–2621.
    1. Liu JK, Yang QW. A new structural damage identification method. Journal of Sound and Vibration. 2006;297(3-5):694–703.
    1. Yang QW, Liu JK. Structural damage identification based on residual force vector. Journal of Sound and Vibration. 2007;305(1-2):298–307.

Publication types

LinkOut - more resources