Rapid evolution of quantitative traits: theoretical perspectives
- PMID: 24454555
- PMCID: PMC3894905
- DOI: 10.1111/eva.12127
Rapid evolution of quantitative traits: theoretical perspectives
Abstract
An increasing number of studies demonstrate phenotypic and genetic changes in natural populations that are subject to climate change, and there is hope that some of these changes will contribute to avoiding species extinctions ('evolutionary rescue'). Here, we review theoretical models of rapid evolution in quantitative traits that can shed light on the potential for adaptation to a changing climate. Our focus is on quantitative-genetic models with selection for a moving phenotypic optimum. We point out that there is no one-to-one relationship between the rate of adaptation and population survival, because the former depends on relative fitness and the latter on absolute fitness. Nevertheless, previous estimates that sustainable rates of genetically based change usually do not exceed 0.1 haldanes (i.e., phenotypic standard deviations per generation) are probably correct. Survival can be greatly facilitated by phenotypic plasticity, and heritable variation in plasticity can further speed up genetic evolution. Multivariate selection and genetic correlations are frequently assumed to constrain adaptation, but this is not necessarily the case and depends on the geometric relationship between the fitness landscape and the structure of genetic variation. Similar conclusions hold for adaptation to shifting spatial gradients. Recent models of adaptation in multispecies communities indicate that the potential for rapid evolution is strongly influenced by interspecific competition.
Keywords: Adaptation; climate change; habitat degradation; natural selection and contemporary evolution; phenotypic plasticity; population dynamics; population genetics; quantitative genetics.
Figures
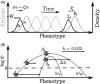
 , variance
, variance  ). The mean phenotype evolves according to eqn (1). At the dynamic equilibrium, it follows the optimum with a constant lag
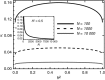
). The mean phenotype evolves according to eqn (1). At the dynamic equilibrium, it follows the optimum with a constant lag  . (B) illustrates the relation between rate of evolution and extinction risk. The gray curves show the log mean fitness as a function of the mean phenotype
. (B) illustrates the relation between rate of evolution and extinction risk. The gray curves show the log mean fitness as a function of the mean phenotype  for two different fitness functions with widths ωs and ωw, respectively. The rate of evolution, given by the horizontal arrows is determined by the fitness gradient βt, indicated by the black lines. The vertical position of the population gives its mean (log) fitness. In the Figure, the optimum is assumed to move at rate k = 0.035, and the population placed at the narrow fitness curve follows at this pace while maintaining a positive growth rate (
for two different fitness functions with widths ωs and ωw, respectively. The rate of evolution, given by the horizontal arrows is determined by the fitness gradient βt, indicated by the black lines. The vertical position of the population gives its mean (log) fitness. In the Figure, the optimum is assumed to move at rate k = 0.035, and the population placed at the narrow fitness curve follows at this pace while maintaining a positive growth rate ( ). With the wide fitness function, however, the same rate of evolution requires a larger distance from the optimum, such that the growth rate is negative and the population goes extinct.
). With the wide fitness function, however, the same rate of evolution requires a larger distance from the optimum, such that the growth rate is negative and the population goes extinct.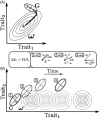
 and whose axis is the eigenvectors of G. The initial response to selection is biased toward the leading eigenvector, that is, the genetic line of least resistance (Schluter 1996). (B) Adaptation to a moving optimum. Gray circles show the fitness landscape at four different points in time. Black ellipses show the corresponding positions of the population (represented by the G-matrix). The insets at the top show the leading eigenvector of G, λ1, the selection gradient βt and the response to selection
and whose axis is the eigenvectors of G. The initial response to selection is biased toward the leading eigenvector, that is, the genetic line of least resistance (Schluter 1996). (B) Adaptation to a moving optimum. Gray circles show the fitness landscape at four different points in time. Black ellipses show the corresponding positions of the population (represented by the G-matrix). The insets at the top show the leading eigenvector of G, λ1, the selection gradient βt and the response to selection  at time points 1, 2, and 3, respectively. Because the initial response is biased toward the leading eigenvector, the population ‘rises’ above the line of the moving optimum (i.e., the flying-kite effect; Jones et al. 2004). This rise comes to a halt as the tendency to follow the line of least resistance is balanced by the selection gradient, resulting in horizontal movement of the population.
at time points 1, 2, and 3, respectively. Because the initial response is biased toward the leading eigenvector, the population ‘rises’ above the line of the moving optimum (i.e., the flying-kite effect; Jones et al. 2004). This rise comes to a halt as the tendency to follow the line of least resistance is balanced by the selection gradient, resulting in horizontal movement of the population.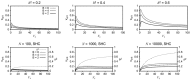
 (with
(with  ), for various values of the reproductive potential B. The top row shows results for three different values of heritability
), for various values of the reproductive potential B. The top row shows results for three different values of heritability  . In the bottom row,
. In the bottom row,  has been set to the value predicted by the stochastic house-of-cards (SHC) approximation under pure stabilizing selection for three values of the population size N. The SHC approximation is given by
has been set to the value predicted by the stochastic house-of-cards (SHC) approximation under pure stabilizing selection for three values of the population size N. The SHC approximation is given by  (Bürger and Lynch 1995), where Vm is the mutational variance, α2 is the variance of the effect of new mutations, and Ne ≈ 2BN / (2B−1) (Bürger and Lynch 1995) is the effective population size. The figures are for Vm = 0.001 and α2 = 0.05. The thin dotted line gives the heritability h2 associated with
(Bürger and Lynch 1995), where Vm is the mutational variance, α2 is the variance of the effect of new mutations, and Ne ≈ 2BN / (2B−1) (Bürger and Lynch 1995) is the effective population size. The figures are for Vm = 0.001 and α2 = 0.05. The thin dotted line gives the heritability h2 associated with  (SHC).
(SHC).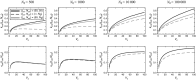
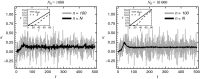
 and the phenotypic optimum zopt. The spike in κ around generation 40, which partially closes the large initial phenotypic lag (insert), is due to an increase in genetic variance (see main text). Fluctuations in the black line reflect genetic drift and environmental variance, whereas those in the gray line are largely due to sampling effects. In addition, rates measured in haldanes vary due to fluctuations in the phenotypic variance
and the phenotypic optimum zopt. The spike in κ around generation 40, which partially closes the large initial phenotypic lag (insert), is due to an increase in genetic variance (see main text). Fluctuations in the black line reflect genetic drift and environmental variance, whereas those in the gray line are largely due to sampling effects. In addition, rates measured in haldanes vary due to fluctuations in the phenotypic variance  (for potential problems of scale, see Hereford et al. ; Hansen and Houle 2008).
(for potential problems of scale, see Hereford et al. ; Hansen and Houle 2008).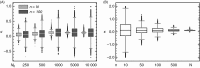
 and
and  , respectively (see main text), as a function of heritability h2 and population size N = Ne (inset). Environmental variance
, respectively (see main text), as a function of heritability h2 and population size N = Ne (inset). Environmental variance  refers to the phenotypic variance caused by developmental instability and micro-environmental fluctuations.
refers to the phenotypic variance caused by developmental instability and micro-environmental fluctuations.References
-
- Alleaume-Benharira M, Pen IR, Ronce O. Geographical patterns of adaptation within a species' range: interactions between drift and gene flow. Journal of Evolutionary Biology. 2006;19:203–215. - PubMed
-
- Alvarez-Castro JM, Kopp M, Hermisson J. Effects of epistasis and the evolution of genetic architecture: exact results for a 2-locus model. Theoretical Population Biology. 2009;75:109–122. - PubMed
-
- Amarasekare P, Savage V. A framework for elucidating the temperature dependence of fitness. American Naturalist. 2012;179:178–191. - PubMed
-
- Ancel LW. A quantitative model of the Simpson-Baldwin effect. Journal of Theoretical Biology. 1999;196:197–209. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

