Emergence of connectivity motifs in networks of model neurons with short- and long-term plastic synapses
- PMID: 24454735
- PMCID: PMC3893143
- DOI: 10.1371/journal.pone.0084626
Emergence of connectivity motifs in networks of model neurons with short- and long-term plastic synapses
Abstract
Recent experimental data from the rodent cerebral cortex and olfactory bulb indicate that specific connectivity motifs are correlated with short-term dynamics of excitatory synaptic transmission. It was observed that neurons with short-term facilitating synapses form predominantly reciprocal pairwise connections, while neurons with short-term depressing synapses form predominantly unidirectional pairwise connections. The cause of these structural differences in excitatory synaptic microcircuits is unknown. We show that these connectivity motifs emerge in networks of model neurons, from the interactions between short-term synaptic dynamics (SD) and long-term spike-timing dependent plasticity (STDP). While the impact of STDP on SD was shown in simultaneous neuronal pair recordings in vitro, the mutual interactions between STDP and SD in large networks are still the subject of intense research. Our approach combines an SD phenomenological model with an STDP model that faithfully captures long-term plasticity dependence on both spike times and frequency. As a proof of concept, we first simulate and analyze recurrent networks of spiking neurons with random initial connection efficacies and where synapses are either all short-term facilitating or all depressing. For identical external inputs to the network, and as a direct consequence of internally generated activity, we find that networks with depressing synapses evolve unidirectional connectivity motifs, while networks with facilitating synapses evolve reciprocal connectivity motifs. We then show that the same results hold for heterogeneous networks, including both facilitating and depressing synapses. This does not contradict a recent theory that proposes that motifs are shaped by external inputs, but rather complements it by examining the role of both the external inputs and the internally generated network activity. Our study highlights the conditions under which SD-STDP might explain the correlation between facilitation and reciprocal connectivity motifs, as well as between depression and unidirectional motifs.
Conflict of interest statement
Figures
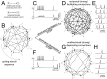
 pA, and Methods.
pA, and Methods.
 times, each time starting from a random initial topology. STDP progressively induced a persisting non-random reconfiguration of strong connections, quantified across time by a symmetry index (see Methods). Neurons connected only by short-term depressing synapses evolved strong unidirectional connections, corresponding to a low symmetry index. This is displayed in panel C, as an average across the
times, each time starting from a random initial topology. STDP progressively induced a persisting non-random reconfiguration of strong connections, quantified across time by a symmetry index (see Methods). Neurons connected only by short-term depressing synapses evolved strong unidirectional connections, corresponding to a low symmetry index. This is displayed in panel C, as an average across the  simulations (left panel). Initial and final distributions of symmetry index values are also shown (right panel, grey and black histogram respectively). Neurons connected only by short-term facilitating synapses evolved instead strong bidirectional connections with high symmetry indexes (D).
simulations (left panel). Initial and final distributions of symmetry index values are also shown (right panel, grey and black histogram respectively). Neurons connected only by short-term facilitating synapses evolved instead strong bidirectional connections with high symmetry indexes (D).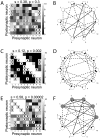
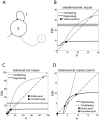
 . Excitatory and inhibitory external inputs are modeled by a single term, taking positive, zero or negative values. A zero value corresponds to balanced excitatory/inhibitory inputs, while a non-zero value corresponds to unbalanced excitatory/inhibitory inputs. The steady-state firing rate (i.e.,
. Excitatory and inhibitory external inputs are modeled by a single term, taking positive, zero or negative values. A zero value corresponds to balanced excitatory/inhibitory inputs, while a non-zero value corresponds to unbalanced excitatory/inhibitory inputs. The steady-state firing rate (i.e.,  , in a.u.) are the roots of the equation
, in a.u.) are the roots of the equation  (see Text S1), whose graphical solution is provided (B–D), for facilitating (grey) or depressing (black) synapses, without long-term plasticity. Panel D is a zoomed view of C. (Un)stable firing rate equilibria are indicated by filled circles (squares). Networks with facilitating synapses fire at higher rates than networks with depressing synapses, as emphasized by the grey shading.
(see Text S1), whose graphical solution is provided (B–D), for facilitating (grey) or depressing (black) synapses, without long-term plasticity. Panel D is a zoomed view of C. (Un)stable firing rate equilibria are indicated by filled circles (squares). Networks with facilitating synapses fire at higher rates than networks with depressing synapses, as emphasized by the grey shading.
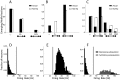
 Integrate-and-Fire model neurons were numerically simulated, under identical conditions. Panel A shows the comparison of the emergence of weak or no connectivity pairs (indicated as “-, -”), of unidirectional strong connectivity pairs (“
Integrate-and-Fire model neurons were numerically simulated, under identical conditions. Panel A shows the comparison of the emergence of weak or no connectivity pairs (indicated as “-, -”), of unidirectional strong connectivity pairs (“ ”, “D, -”), and of reciprocal strong connectivity pairs (“
”, “D, -”), and of reciprocal strong connectivity pairs (“ ”, “D, D”) for a homogeneous network of neurons connected by depressing synapses: strong unidirectional depressing connections significantly outnumber reciprocal depressing ones. The fractions of emerged motifs (black) is significantly different than the null hypothesis (white) of random motifs occurrence. Panel B repeats this quantification for a homogeneous network with facilitating synapses: strong connections are found only on reciprocal connectivity pairs (“
”, “D, D”) for a homogeneous network of neurons connected by depressing synapses: strong unidirectional depressing connections significantly outnumber reciprocal depressing ones. The fractions of emerged motifs (black) is significantly different than the null hypothesis (white) of random motifs occurrence. Panel B repeats this quantification for a homogeneous network with facilitating synapses: strong connections are found only on reciprocal connectivity pairs (“ ”, “F, F”) and all emerging motifs are non-random. Panel C repeats the same quantification for a heterogeneous network with both short-term facilitating and depressing synapses. Emerging motifs display highly non-random features and confirm that reciprocal facilitatory motifs (“
”, “F, F”) and all emerging motifs are non-random. Panel C repeats the same quantification for a heterogeneous network with both short-term facilitating and depressing synapses. Emerging motifs display highly non-random features and confirm that reciprocal facilitatory motifs (“ ”, “F, F”) outnumber unidirectional facilitatory motifs (“
”, “F, F”) outnumber unidirectional facilitatory motifs (“ ”, “F, -”), and that unidirectional depressing motifs (“
”, “F, -”), and that unidirectional depressing motifs (“ ”, “D,-”) outnumber reciprocal depressing motifs (“
”, “D,-”) outnumber reciprocal depressing motifs (“ ”, “D, D”). Panels D–F display the steady-state firing rate distributions, corresponding to homogeneous depressing, homogeneous facilitating, and heterogeneous networks respectively. The plots confirm that heterogeneity in connectivity motifs is accompanied by bimodal firing rates above and below the critical frequency, represented here by a grey shading.
”, “D, D”). Panels D–F display the steady-state firing rate distributions, corresponding to homogeneous depressing, homogeneous facilitating, and heterogeneous networks respectively. The plots confirm that heterogeneity in connectivity motifs is accompanied by bimodal firing rates above and below the critical frequency, represented here by a grey shading.
 ,
,  ,
,  , and
, and  , undergo long-term modification. Panels B, D show the long-term changes of an isolated synapse (decoupled from recurrent interactions) depending on pre- and postsynaptic spike timing (i.e.,
, undergo long-term modification. Panels B, D show the long-term changes of an isolated synapse (decoupled from recurrent interactions) depending on pre- and postsynaptic spike timing (i.e.,  ,
,  ) and frequencies (i.e.,
) and frequencies (i.e.,  ,
,  ). When
). When  and
and  are varied independently, long-term potentiation (LTP) and depression (LTD) emerge as in associative Hebbian plasticity. This suggests that
are varied independently, long-term potentiation (LTP) and depression (LTD) emerge as in associative Hebbian plasticity. This suggests that  and
and  will become significantly stronger than
will become significantly stronger than  and
and  (C) and that such a configuration will be retained indefinitely. This was confirmed by simulations (E–F) plotting the temporal evolution of the firing rates
(C) and that such a configuration will be retained indefinitely. This was confirmed by simulations (E–F) plotting the temporal evolution of the firing rates  (black trace) and
(black trace) and  (grey trace), and of the mean synaptic efficacies
(grey trace), and of the mean synaptic efficacies  (F). The heterogeneity occurs by separation of emerging firing rates (Fig. 4), as emphasized by the grey shading. Parameters:
(F). The heterogeneity occurs by separation of emerging firing rates (Fig. 4), as emphasized by the grey shading. Parameters:  ,
,  msec, with initial conditions for the maximal synaptic efficacies
msec, with initial conditions for the maximal synaptic efficacies  , and
, and  . Please note that without loss of generality we fix
. Please note that without loss of generality we fix  .
.
 of connecting to its postsynaptic target by a depressing synapse, and
of connecting to its postsynaptic target by a depressing synapse, and  of connecting to its target by a facilitating synapticapse. Panel B plots the location of the equilibria of the firing rate
of connecting to its target by a facilitating synapticapse. Panel B plots the location of the equilibria of the firing rate  , under distinct external inputs conditions and for increasing values of
, under distinct external inputs conditions and for increasing values of  . For the same parameters of Fig. 4, stable equilibria move as a function of
. For the same parameters of Fig. 4, stable equilibria move as a function of  , taking intermediate values between the two extreme cases, i.e.,
, taking intermediate values between the two extreme cases, i.e.,  and
and  ; compare to panels D–F of Figs. 4 .
; compare to panels D–F of Figs. 4 .Similar articles
-
Autonomous emergence of connectivity assemblies via spike triplet interactions.PLoS Comput Biol. 2020 May 8;16(5):e1007835. doi: 10.1371/journal.pcbi.1007835. eCollection 2020 May. PLoS Comput Biol. 2020. PMID: 32384081 Free PMC article.
-
Self-Organization of Microcircuits in Networks of Spiking Neurons with Plastic Synapses.PLoS Comput Biol. 2015 Aug 20;11(8):e1004458. doi: 10.1371/journal.pcbi.1004458. eCollection 2015 Aug. PLoS Comput Biol. 2015. PMID: 26291697 Free PMC article.
-
Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. II. Input selectivity--symmetry breaking.Biol Cybern. 2009 Aug;101(2):103-14. doi: 10.1007/s00422-009-0320-y. Epub 2009 Jun 18. Biol Cybern. 2009. PMID: 19536559
-
Propagation delays determine neuronal activity and synaptic connectivity patterns emerging in plastic neuronal networks.Chaos. 2018 Oct;28(10):106308. doi: 10.1063/1.5037309. Chaos. 2018. PMID: 30384625 Review.
-
Neuronal networks and synaptic plasticity: understanding complex system dynamics by interfacing neurons with silicon technologies.J Exp Biol. 2006 Jun;209(Pt 12):2312-9. doi: 10.1242/jeb.02163. J Exp Biol. 2006. PMID: 16731807 Review.
Cited by
-
Abstract concept learning in a simple neural network inspired by the insect brain.PLoS Comput Biol. 2018 Sep 17;14(9):e1006435. doi: 10.1371/journal.pcbi.1006435. eCollection 2018 Sep. PLoS Comput Biol. 2018. PMID: 30222735 Free PMC article.
-
Discrimination of Motion Direction in a Robot Using a Phenomenological Model of Synaptic Plasticity.Comput Intell Neurosci. 2019 May 2;2019:6989128. doi: 10.1155/2019/6989128. eCollection 2019. Comput Intell Neurosci. 2019. PMID: 31191633 Free PMC article.
-
Recurrently connected and localized neuronal communities initiate coordinated spontaneous activity in neuronal networks.PLoS Comput Biol. 2017 Jul 27;13(7):e1005672. doi: 10.1371/journal.pcbi.1005672. eCollection 2017 Jul. PLoS Comput Biol. 2017. PMID: 28749937 Free PMC article.
-
Adaptation of short-term plasticity parameters via error-driven learning may explain the correlation between activity-dependent synaptic properties, connectivity motifs and target specificity.Front Comput Neurosci. 2015 Jan 29;8:175. doi: 10.3389/fncom.2014.00175. eCollection 2014. Front Comput Neurosci. 2015. PMID: 25688203 Free PMC article.
-
Autonomous emergence of connectivity assemblies via spike triplet interactions.PLoS Comput Biol. 2020 May 8;16(5):e1007835. doi: 10.1371/journal.pcbi.1007835. eCollection 2020 May. PLoS Comput Biol. 2020. PMID: 32384081 Free PMC article.
References
-
- Seung H (2009) Reading the book of memory: Sparse sampling reading the book of memory: Sparse sampling versus dense mapping of connectomes. Neuron 62: 17–29. - PubMed
-
- Wang Y, Markram H, Goodman P, Berger T, Ma J, et al. (2006) Heterogeneity in the pyramidal network of the medial prefrontal cortex. Nat Neurosci 9: 534–42. - PubMed
-
- Silberberg G, Markram H (2007) Disynaptic inhibition between neocortical pyramidal cells mediated by martinotti cells. Neuron 53: 735–46. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases
Research Materials

