The fiber walk: a model of tip-driven growth with lateral expansion
- PMID: 24465607
- PMCID: PMC3899046
- DOI: 10.1371/journal.pone.0085585
The fiber walk: a model of tip-driven growth with lateral expansion
Abstract
Tip-driven growth processes underlie the development of many plants. To date, tip-driven growth processes have been modeled as an elongating path or series of segments, without taking into account lateral expansion during elongation. Instead, models of growth often introduce an explicit thickness by expanding the area around the completed elongated path. Modeling expansion in this way can lead to contradictions in the physical plausibility of the resulting surface and to uncertainty about how the object reached certain regions of space. Here, we introduce fiber walks as a self-avoiding random walk model for tip-driven growth processes that includes lateral expansion. In 2D, the fiber walk takes place on a square lattice and the space occupied by the fiber is modeled as a lateral contraction of the lattice. This contraction influences the possible subsequent steps of the fiber walk. The boundary of the area consumed by the contraction is derived as the dual of the lattice faces adjacent to the fiber. We show that fiber walks generate fibers that have well-defined curvatures, and thus enable the identification of the process underlying the occupancy of physical space. Hence, fiber walks provide a base from which to model both the extension and expansion of physical biological objects with finite thickness.
Conflict of interest statement
Figures
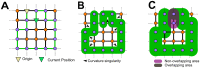
 of an edge length - multiple regions in space are “associated” with different steps, leading to an identifiability problem, which holds for all thickening greater than or equal to
of an edge length - multiple regions in space are “associated” with different steps, leading to an identifiability problem, which holds for all thickening greater than or equal to  of an edge length.
of an edge length.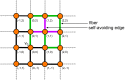
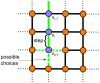
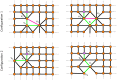
 (compare Fig. 3). Here the chosen edge to reach
(compare Fig. 3). Here the chosen edge to reach  is shown in green. Selection of vertices incident to the walk from the side correspond to the expansion. The vertices selected to be merged with
is shown in green. Selection of vertices incident to the walk from the side correspond to the expansion. The vertices selected to be merged with  are shown in grey. Contraction of the selected vertices and its result after merging the selected vertices to
are shown in grey. Contraction of the selected vertices and its result after merging the selected vertices to  . Another step, including elongation and expansion, is shown as a second step on the lattice. The second step reaching
. Another step, including elongation and expansion, is shown as a second step on the lattice. The second step reaching  uses the same color schema as before.
uses the same color schema as before.
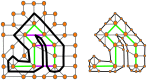
 and 2. In both figures the edge labels involved in the contraction and their direction, indicated as arrows are shown.
and 2. In both figures the edge labels involved in the contraction and their direction, indicated as arrows are shown.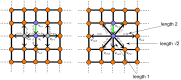
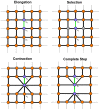
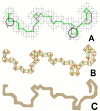
 and Case 2b shows a self-avoiding edge of length 3. The fiber on a lattice is colored green and its edges selected for contraction are shown in grey. The dotted green line denotes an unknown fiber walk that is not affecting the given configuration. In both figures the edge labels involved in the contraction and their direction indicated as arrows are shown.
and Case 2b shows a self-avoiding edge of length 3. The fiber on a lattice is colored green and its edges selected for contraction are shown in grey. The dotted green line denotes an unknown fiber walk that is not affecting the given configuration. In both figures the edge labels involved in the contraction and their direction indicated as arrows are shown.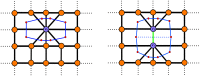
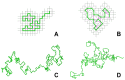

References
-
- Rounds CM, Bezanilla M (2013) Growth mechanisms in tip-growing plant cells. Annual review of plant biology 64: 243–265. - PubMed
-
- Madras N, Slade G (1993) The self-avoiding walk. probability and its applications. Birkhauser Boston Inc, Boston, MA 49: 105.
-
- Landau DP, Binder K (2009) A guide to monte carlo simulations in statistical physics.
-
- Karch R, Neumann F, Neumann M, Schreiner W (1999) A three-dimensional model for arterial tree representation, generated by constrained constructive optimization. Computers in biology and medicine 29: 19–38. - PubMed
-
- Hamarneh G, Jassi P (2010) ¡ i¿ vascusynth¡/i¿: Simulating vascular trees for generating volumetric image data with ground-truth segmentation and tree analysis. Computerized medical imaging and graphics 34: 605–616. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

