GENERALIZED DOUBLE PARETO SHRINKAGE

Abstract

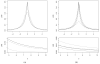
We propose a generalized double Pareto prior for Bayesian shrinkage estimation and inferences in linear models. The prior can be obtained via a scale mixture of Laplace or normal distributions, forming a bridge between the Laplace and Normal-Jeffreys' priors. While it has a spike at zero like the Laplace density, it also has a Student's t-like tail behavior. Bayesian computation is straightforward via a simple Gibbs sampling algorithm. We investigate the properties of the maximum a posteriori estimator, as sparse estimation plays an important role in many problems, reveal connections with some well-established regularization procedures, and show some asymptotic results. The performance of the prior is tested through simulations and an application.

Keywords: Heavy tails; LASSO; high-dimensional data; maximum a posteriori estimation; relevance vector machine; robust prior; shrinkage estimation.

Figure 2.1

(a) Probability density functions for standard double Pareto (solid line), standard Cauchy (dashed line) and Laplace (dot-dash line) (λ = 1) distributions. (b) Probability density functions for the generalized double Pareto with (ξ, α) values of (1, 1) (solid line), (0.5, 1) (dashed line), (1, 3) (long-dashed line), and (3, 1) (dot-dash line).

Figure 2.2

Prior density of κ implied by the standard double Pareto prior (solid line), Strawderman–Berger prior (dashed line), horseshoe prior (dot-dash line) and standard Cauchy prior (dotted line).

Figure 2.3

Prior density of κ (a) when α = 1 and η = 0.5 (dashed), η = 1 (solid), η = 2 (dot-dash) (b) when η = 1 and α = 1 (solid), α = 2 (dashed), α = 3 (dot-dash).

Figure 4.4

Thresholding functions for (a) generalized double Pareto prior with $\eta =\sqrt{\alpha +1}$, α = {1, 3, 7}, (b) Hard thresholding, generalized double Pareto prior with η = 2, α = 3 and LASSO with σ = 1.

Figure 4.5

Number of iterations until convergence of the EM algorithms under normal and Laplace representations.

Figure 5.6

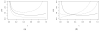
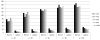
Inferences for (a) GDP(PM) for n = 50 under Model 2, (b) GDP(PM)² for n = 50 under Model 2, (c) GDP(PM) for n = 400 under Model 2, (b) GDP(PM)² for n = 400 under Model 2, (e) GDP(PM) for n = 50 under Model 5, (f) GDP(PM)² for n = 50 under Model 5, (g) GDP(PM) for n = 400 under Model 5, (h) GDP(PM)² for n = 400 under Model 2.

Figure 6.7

The correlation structure of the Ozone data.

Figure 6.8

Out-of-sample performance comparisons for Ozone data. (×) denotes the median value for ${\text{R}}_{\text{test}}^2$ while the lines represent the ±2 standard error regions. ¹α = 1, η = 1; ²η = 1.