Interplay of population genetics and dynamics in the genetic control of mosquitoes
- PMID: 24522781
- PMCID: PMC3928937
- DOI: 10.1098/rsif.2013.1071
Interplay of population genetics and dynamics in the genetic control of mosquitoes
Abstract
Some proposed genetics-based vector control methods aim to suppress or eliminate a mosquito population in a similar manner to the sterile insect technique. One approach under development in Anopheles mosquitoes uses homing endonuclease genes (HEGs)-selfish genetic elements (inherited at greater than Mendelian rate) that can spread rapidly through a population even if they reduce fitness. HEGs have potential to drive introduced traits through a population without large-scale sustained releases. The population genetics of HEG-based systems has been established using discrete-time mathematical models. However, several ecologically important aspects remain unexplored. We formulate a new continuous-time (overlapping generations) combined population dynamic and genetic model and apply it to a HEG that targets and knocks out a gene that is important for survival. We explore the effects of density dependence ranging from undercompensating to overcompensating larval competition, occurring before or after HEG fitness effects, and consider differences in competitive effect between genotypes (wild-type, heterozygotes and HEG homozygotes). We show that population outcomes-elimination, suppression or loss of the HEG-depend crucially on the interaction between these ecological aspects and genetics, and explain how the HEG fitness properties, the homing rate (drive) and the insect's life-history parameters influence those outcomes.
Keywords: genetic vector control; homing endonuclease gene; population dynamics; population genetics.
Figures



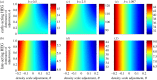
 where oscillating (open symbols), for the spectrum of values of homing rate 0 ≤ g ≤ 1 (g = 0 results in wild-type population). The HEG is recessive lethal (s = 1, h = 0), early-acting (a) or late-acting (b). Strength of density dependence b is 0.5, 1.097, 2.5, 3 or 5 (key in a). Pre-release equilibrium N* = 60 per host for all values of b; in unstable natural populations, the pre-release average
where oscillating (open symbols), for the spectrum of values of homing rate 0 ≤ g ≤ 1 (g = 0 results in wild-type population). The HEG is recessive lethal (s = 1, h = 0), early-acting (a) or late-acting (b). Strength of density dependence b is 0.5, 1.097, 2.5, 3 or 5 (key in a). Pre-release equilibrium N* = 60 per host for all values of b; in unstable natural populations, the pre-release average  is higher than 60 (the same value as with g = 0).
is higher than 60 (the same value as with g = 0).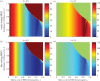
References
-
- WHO. 2011. World malaria report 2011. Geneva, Switzerland: World Health Organization.
-
- WHO. 2008. The global burden of disease: 2004 update: deaths and DALYs 2004: annex tables Geneva, Switzerland: World Health Organization.
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

