Interfibrillar shear stress is the loading mechanism of collagen fibrils in tendon
- PMID: 24530560
- PMCID: PMC4034159
- DOI: 10.1016/j.actbio.2014.01.032
Interfibrillar shear stress is the loading mechanism of collagen fibrils in tendon
Abstract
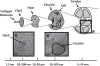
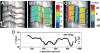
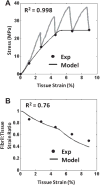
Despite the critical role tendons play in transmitting loads throughout the musculoskeletal system, little is known about the microstructural mechanisms underlying their mechanical function. Of particular interest is whether collagen fibrils in tendon fascicles bear load independently or if load is transferred between fibrils through interfibrillar shear forces. We conducted multiscale experimental testing and developed a microstructural shear lag model to explicitly test whether interfibrillar shear load transfer is indeed the fibrillar loading mechanism in tendon. Experimental correlations between fascicle macroscale mechanics and microscale interfibrillar sliding suggest that fibrils are discontinuous and share load. Moreover, for the first time, we demonstrate that a shear lag model can replicate the fascicle macroscale mechanics as well as predict the microscale fibrillar deformations. Since interfibrillar shear stress is the fundamental loading mechanism assumed in the model, this result provides strong evidence that load is transferred between fibrils in tendon and possibly other aligned collagenous tissues. Conclusively establishing this fibrillar loading mechanism and identifying the involved structural components should help develop repair strategies for tissue degeneration and guide the design of tissue engineered replacements.
Keywords: Fibril sliding; Interfibrillar shear stress; Multiscale testing; Shear lag model; Tendon.
Copyright © 2014 Acta Materialia Inc. Published by Elsevier Ltd. All rights reserved.
Figures



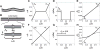
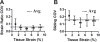

References
-
- Kastelic J, Galeski A, Baer E. The multicomposite structure of tendon. Connect Tissue Res. 1978;6:11–23. - PubMed
-
- Rowe RW. The structure of rat tail tendon. Connect Tissue Res. 1985;14:9–20. - PubMed
-
- Torp S, Baer E, Friedman B. Effects of age and of mechanical deformation on the ultrastructure of tendon. In: Atkins ED, Keller A, editors. Structure of fibrous biopolymers. London: Colston Research Society; 1975. pp. 223–50.
-
- Lanir Y. Constitutive equations for fibrous connective tissues. J Biomech. 1983;16:1–12. - PubMed
-
- Cook JL, Purdam CR. Is tendon pathology a continuum? A pathology model to explain the clinical presentation of load-induced tendinopathy. Br J Sports Med. 2009;43:409–16. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

