A penalized-likelihood method to estimate the distribution of selection coefficients from phylogenetic data

Abstract

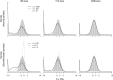
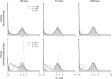
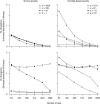
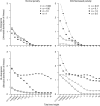
We develop a maximum penalized-likelihood (MPL) method to estimate the fitnesses of amino acids and the distribution of selection coefficients (S = 2Ns) in protein-coding genes from phylogenetic data. This improves on a previous maximum-likelihood method. Various penalty functions are used to penalize extreme estimates of the fitnesses, thus correcting overfitting by the previous method. Using a combination of computer simulation and real data analysis, we evaluate the effect of the various penalties on the estimation of the fitnesses and the distribution of S. We show the new method regularizes the estimates of the fitnesses for small, relatively uninformative data sets, but it can still recover the large proportion of deleterious mutations when present in simulated data. Computer simulations indicate that as the number of taxa in the phylogeny or the level of sequence divergence increases, the distribution of S can be more accurately estimated. Furthermore, the strength of the penalty can be varied to study how informative a particular data set is about the distribution of S. We analyze three protein-coding genes (the chloroplast rubisco protein, mammal mitochondrial proteins, and an influenza virus polymerase) and show the new method recovers a large proportion of deleterious mutations in these data, even under strong penalties, confirming the distribution of S is bimodal in these real data. We recommend the use of the new MPL approach for the estimation of the distribution of S in species phylogenies of protein-coding genes.

Keywords: chloroplast; fitness effects; influenza; mitochondria; penalized likelihood; selection coefficient.

Figure 1

Marginal distribution density of F_i when θ = (θ_i) ∼ Dirichlet(θ | α). The marginal density of θ_i is f(θ_i) = Beta(θ_i | α, αk − α), and the marginal density of F_i is f(F_i) = f(θ_i) × J = Beta(θ_i | α, αk − α) × θ_i(1 − θ_i), with θ_i = exp F_i/(k − 1 + exp F_i). A Dirichlet distribution with α = 1 is very informative on the transformed parameter space on F: The 95% equal-tail range of θ_i is (0.00133, 0.176), corresponding to a 95% range for F_i of (−3.68, 1.41).

Figure 2

Estimated and true distribution of S (for nonsynonymous mutations) for simulated data when the fitnesses are sampled from a unimodal distribution. The true distribution is shown as vertical shaded bars. The distributions are calculated using Equation 4 by dividing the range of S from −10 to 10 into equally spaced bins with w_I = 0.25. Mutations with S ≤ −10 or those with S ≥ 10 are binned together. We consider mutations to STOP codons to be lethal, and these are included in the calculation of h(−10).

Figure 3

Estimated and true distribution of S (for nonsynonymous mutations) for simulated data when the fitnesses are sampled from a bimodal distribution. The true distribution is shown as vertical shaded bars. The distributions are calculated as in Figure 2.

Figure 4

Kullback–Leibler divergence between the true distribution of S (for nonsynonymous mutations) and its estimate vs. number of taxa for simulated data sets.

Figure 5

Kullback–Leibler divergence between the true distribution of S (for nonsynonymous mutations) and its estimate as a function of total tree height of a 4096-taxon tree.

Figure 6

Estimated distribution of S (for nonsynonymous mutations) for real data sets. The D_KL distance is calculated with Equation 12, with h₀ being the weaker penalty. The distributions are calculated using Equation 4, setting w_I = 0.25 for all I.