Modelling individual differences in the form of Pavlovian conditioned approach responses: a dual learning systems approach with factored representations

Abstract

Reinforcement Learning has greatly influenced models of conditioning, providing powerful explanations of acquired behaviour and underlying physiological observations. However, in recent autoshaping experiments in rats, variation in the form of Pavlovian conditioned responses (CRs) and associated dopamine activity, have questioned the classical hypothesis that phasic dopamine activity corresponds to a reward prediction error-like signal arising from a classical Model-Free system, necessary for Pavlovian conditioning. Over the course of Pavlovian conditioning using food as the unconditioned stimulus (US), some rats (sign-trackers) come to approach and engage the conditioned stimulus (CS) itself - a lever - more and more avidly, whereas other rats (goal-trackers) learn to approach the location of food delivery upon CS presentation. Importantly, although both sign-trackers and goal-trackers learn the CS-US association equally well, only in sign-trackers does phasic dopamine activity show classical reward prediction error-like bursts. Furthermore, neither the acquisition nor the expression of a goal-tracking CR is dopamine-dependent. Here we present a computational model that can account for such individual variations. We show that a combination of a Model-Based system and a revised Model-Free system can account for the development of distinct CRs in rats. Moreover, we show that revising a classical Model-Free system to individually process stimuli by using factored representations can explain why classical dopaminergic patterns may be observed for some rats and not for others depending on the CR they develop. In addition, the model can account for other behavioural and pharmacological results obtained using the same, or similar, autoshaping procedures. Finally, the model makes it possible to draw a set of experimental predictions that may be verified in a modified experimental protocol. We suggest that further investigation of factored representations in computational neuroscience studies may be useful.

Figure 1. Computational representation of the autoshaping procedure.

(A) MDP accounting for the experiments described in , , , . States are described by a set of variables: L/F - Lever/Food is available, cM/cL - close to the Magazine/Lever, La - Lever appearance. The initial state is double circled, the dashed state is terminal and ends the current episode. Actions are engage with the proximal stimuli, explore, or go to the Magazine/Lever and eat. For each action, the feature that is being focused on is displayed within brackets. The path that STs should favour is in red. The path that GTs should favour is in dashed blue. (B) Time line corresponding to the unfolding of the MDP.

Figure 2. General architecture of the model and variants.

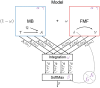
The model is composed of a Model-Based system (MB, in blue) and a Feature-Model-Free system (FMF, in red) which provide respectively an Advantage function and a value function values for actions given a state . These values are integrated in , prior to be used into an action selection mechanism. The various elements may rely on parameters (in purple). The impact of flupentixol on dopamine is represented by a parameter that influences the action selection mechanism and/or any reward prediction error that might be computed in the model.

Figure 3. Summary of simulations and results.

Each line represents a different model composed of a pair of Reinforcement Learning systems. Each column represents a simulated experiment. Experiments are grouped by the kind of data accounted for: behavioural (autoshaping , , CRE , Incentive salience [23], [24]), physiological and pharmacological (Flu post-NAcC , Flu pre-systemic [21]). Variant 4 (i.e. Model-based/Model-Free without features) is not included as it failed to even reproduce the autoshaping behavioural results and was not investigated further.

Figure 4. Summary of the key mechanisms required by the model to reproduce experimental results.

Each line represents a different mechanism of the model. Each column represents a simulated experiment. For each mechanism, it states in which experiment and for which behaviour – sign-tracking (red), goal-tracking (blue) or both (+) – it is required. Note however that all mechanisms and associated parameters have, to a certain extent, an impact on any presented results.

Figure 5. Reproduction of sign- versus goal-tracking tendencies in a population of rats undergoing an autoshaping experiment.

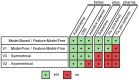
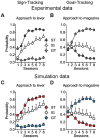
Mean probabilities to engage at least once with the lever (A,C) or the magazine (B,D) during trials. Data are expressed as mean S.E.M. and illustrated in 50-trial (2-session) blocks. (A,B) Reproduction of Flagel et al. experimental results (Figure 2 A,B). Sign-trackers (ST) made the most lever presses (black), goal-trackers (GT) made the least lever presses (white), Intermediate group (IG) is in between (grey). (C,D) Simulation of the same procedure (squares) with the model. Simulated groups of rats are defined as STs (; ; ; ; ; ; ; ; n = 14) in red, GTs ( ; ; ; ; ; ; ; ; n = 14) in blue and IGs (; ; ; ; ; ; ; ; n = 14) in white. The model reproduces the same behavioural tendencies. With training, STs tend to engage more and more with the lever and less with the magazine, while GTs neglect the lever to increasingly engage with the magazine. IGs are in between.

Figure 6. Possible explanation of incentive salience and Conditioned Reinforcement Effect by values learned during autoshaping procedure.

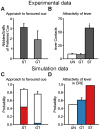
Data are expressed as mean S.E.M. Simulated groups of rats are defined as in Figure 5. (A) Number of nibbles and sniffs of preferred cue by STs and GTs as a measure for incentive salience. Data extracted from Mahler et al. from Figure 3 (bottom-left). (B) Reproduction of Robinson et al. experimental results (Figure 2 B). Lever contacts by STs and GTs during a conditioned reinforcer experiment. (C) Probability to engage with the respective favoured stimuli of STs and GTs at the end of the simulation (white, similar to the last session of Figure 5 C for STs and D for GTs) superimposed with the contribution in percentage of the values attributed by the Feature-Model-Free system in such engagement for STs (red) and GTs (blue). We hypothesize that such value is the source of incentive salience and explains why STs and GTs have a consumption-like behaviour towards their favoured stimulus. (D) Probability to engage with the lever versus exploring when presented with the lever and no magazine for STs (red), GTs (blue) and a random-policy group UN (white), simulating the unpaired group (UN) of the experimental data. Probabilities were computed by applying the softmax function after removing the values for the magazine interactions (see Methods). STs would hence actively seek to engage with the lever relatively to GTs in a Conditioned Reinforcement Effect procedure.

Figure 7. Reproduction of patterns of dopaminergic activity of sign- versus goal-trackers undergoing an autoshaping experiment.

Data are expressed as mean S.E.M. (A,B) Reproduction of Flagel et al. experimental results (Figure 3 d,f). Phasic dopamine release recorded in the core of the nucleus accumbens in STs (light grey) and GTs (grey) using Fast Scan Cyclic Voltammetry. Change in peak amplitude of the dopamine signal observed in response to CS and US presentation for each session of conditioning (C,D) Average RPE computed by the Feature-Model-Free system in response to CS and US presentation for each session of conditioning. Simulated groups of rats are defined as in Figure 5. The model is able to qualitatively reproduce the physiological data. STs (blue) show a shift of activity from US to CS time over training, while GTs develop a second activity at CS time while maintaining the initial activity at US time.

Figure 8. Reproduction of the effect of systemic injections of flupentixol on sign-tracking and goal-tracking behaviours.

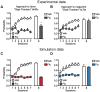
Data are expressed as mean S.E.M. (A,B) Reproduction of Flagel et al. experimental results (Figure 4 a,d). Effects of flupentixol on the probability to approach the lever for STs (A) and the magazine for GTs (B) during lever presentation. (C,D) Simulation of the same procedure (squares) with the model. Simulated groups of rats are defined as in Figure 5. (C) By flattening the softmax temperature and reducing the RPEs of the Feature-Model-Free system, to mimic the possible effect of flupentixol, the model can reproduce the blocked acquisition of sign-tracking in STs (red), engaging less the lever relatively to a saline-injected control group (white). (D) Similarly, the model reproduces that goal-tracking was learned but its expression was blocked. Under flupentixol (first 7 sessions), GTs (blue) did not express goal-tracking, but on a flupentixol-free control test ( session) their engagement with the magazine was almost identical to the engagement of a saline-injected control group (white).

Figure 9. Reproduction of the effect of post injections of flupentixol in the core of the nucleus accumbens.

Data are expressed as mean S.E.M. (A,B) Reproduction of Saunders et al. experimental results (Figure 2 A,D). Effects of different doses of flupentixol on the general tendency to sign-track (A) and goal-track (B) in a population of rats, without discriminating between sign- and goal-trackers. (C,D) Simulation of the same procedure with the model. The simulated population is composed of groups of rats defined as in Figure 5. By simulating the effect of flupentixol as in Figure 8, the model is able to reproduce the decreasing tendency to sign-track in the overall population by increasing the dose of flupentixol.

Figure 10. Characteristics of the Feature-Model-Free system.

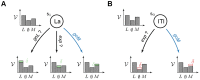
(A) Focusing on a particular feature. The Feature-Model-Free system relies on a value function based on features. Choosing an action (e.g. goL, goM or exp), defines the feature it is focusing on (e.g. Lever, Magazine or nothing ). Once the action is chosen (e.g. goM in blue), only the value of the focused feature (e.g. ) is updated by a standard reward prediction error, while leaving the values of the other features unchanged. (B) Feature-values permit generalization. At a different place and time in the episode, the agent can choose an action (e.g. goM in blue) focusing on a feature (e.g. M) that might have already been focused on. This leads to the revision of the same value (e.g. ) for two different states (e.g. and ). Values of features are shared amongst multiple states.

Figure 11. Systems combined in the model and the variants.

Variants of the model rely on the same architecture (described in Figure 2) and only differ in the combined systems. Colours are shared for similar systems. (A) The model combines a Model-Based system (MB, in blue) and a Feature-Model-Free (FMF, in red) system. (B) Variant 1 combines a Model-Free system (MF, in green) and a Feature-Model-Free system. (C) Variant 2 combines a Model-Free system and a Bias system (BS, in grey), that relies on values from the Model-Free system. (D) Variant 3 combines a Model-Free system and two Bias systems, that rely on values from the Model-Free system. Variant 4 is not included as it failed to even reproduce the autoshaping behavioural results.