Axonal transport: how high microtubule density can compensate for boundary effects in small-caliber axons
- PMID: 24559984
- PMCID: PMC3944719
- DOI: 10.1016/j.bpj.2013.12.047
Axonal transport: how high microtubule density can compensate for boundary effects in small-caliber axons
Abstract
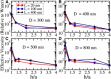
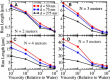
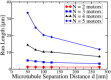
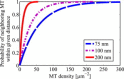
Long-distance intracellular axonal transport is predominantly microtubule-based, and its impairment is linked to neurodegeneration. In this study, we present theoretical arguments that suggest that near the axon boundaries (walls), the effective viscosity can become large enough to impede cargo transport in small (but not large) caliber axons. Our theoretical analysis suggests that this opposition to motion increases rapidly as the cargo approaches the wall. We find that having parallel microtubules close enough together to enable a cargo to simultaneously engage motors on more than one microtubule dramatically enhances motor activity, and thus minimizes the effects of any opposition to transport. Even if microtubules are randomly placed in axons, we find that the higher density of microtubules found in small-caliber axons increases the probability of having parallel microtubules close enough that they can be used simultaneously by motors on a cargo. The boundary effect is not a factor in transport in large-caliber axons where the microtubule density is lower.
Copyright © 2014 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures

Similar articles
-
Axonal Transport: A Constrained System.J Neurol Neuromedicine. 2017;2(3):20-24. doi: 10.29245/2572.942X/2017/3.1118. Epub 2017 Mar 21. J Neurol Neuromedicine. 2017. PMID: 30467560 Free PMC article.
-
MAP2 Defines a Pre-axonal Filtering Zone to Regulate KIF1- versus KIF5-Dependent Cargo Transport in Sensory Neurons.Neuron. 2017 Apr 19;94(2):347-362.e7. doi: 10.1016/j.neuron.2017.03.046. Neuron. 2017. PMID: 28426968
-
One axon, many kinesins: What's the logic?J Neurocytol. 2000 Nov-Dec;29(11-12):799-818. doi: 10.1023/a:1010943424272. J Neurocytol. 2000. PMID: 11466472 Review.
-
Modelling of axonal cargo rerouting in a dendrite.Math Med Biol. 2013 Sep;30(3):273-85. doi: 10.1093/imammb/dqs021. Epub 2012 Jun 1. Math Med Biol. 2013. PMID: 22661115
-
Smart motors and cargo steering drive kinesin-mediated selective transport.Mol Cell Neurosci. 2020 Mar;103:103464. doi: 10.1016/j.mcn.2019.103464. Epub 2020 Jan 20. Mol Cell Neurosci. 2020. PMID: 31972342 Free PMC article. Review.
Cited by
-
Mitochondrial dynamics involves molecular and mechanical events in motility, fusion and fission.Front Cell Dev Biol. 2022 Oct 19;10:1010232. doi: 10.3389/fcell.2022.1010232. eCollection 2022. Front Cell Dev Biol. 2022. PMID: 36340034 Free PMC article. Review.
-
A conceptual view at microtubule plus end dynamics in neuronal axons.Brain Res Bull. 2016 Sep;126(Pt 3):226-237. doi: 10.1016/j.brainresbull.2016.08.006. Epub 2016 Aug 12. Brain Res Bull. 2016. PMID: 27530065 Free PMC article. Review.
-
Axonal Transport: A Constrained System.J Neurol Neuromedicine. 2017;2(3):20-24. doi: 10.29245/2572.942X/2017/3.1118. Epub 2017 Mar 21. J Neurol Neuromedicine. 2017. PMID: 30467560 Free PMC article.
-
The axonal cytoskeleton: from organization to function.Front Mol Neurosci. 2015 Aug 14;8:44. doi: 10.3389/fnmol.2015.00044. eCollection 2015. Front Mol Neurosci. 2015. PMID: 26321907 Free PMC article. Review.
-
Direct Photobiomodulation Therapy on the Sciatic Nerve Significantly Attenuates Acute Nociceptive Sensitivity Without Affecting Motor Output.Neuromodulation. 2024 Dec;27(8):1338-1346. doi: 10.1016/j.neurom.2024.04.011. Epub 2024 Jul 2. Neuromodulation. 2024. PMID: 38958630 Free PMC article.
References
-
- De Vos K.J., Grierson A.J., Miller C.C. Role of axonal transport in neurodegenerative diseases. Annu. Rev. Neurosci. 2008;31:151–173. - PubMed
-
- Fadić R., Vergara J., Alvarez J. Microtubules and caliber of central and peripheral processes of sensory axons. J. Comp. Neurol. 1985;236:258–264. - PubMed
-
- Pannese E., Ledda M., Procacci P. A comparison of the density of microtubules in the central and peripheral axonal branches of the pseudounipolar neurons of lizard spinal ganglia. Anat. Rec. 1984;208:595–605. - PubMed
-
- Malbouisson A.M., Ghabriel M.N., Allt G. Axonal microtubules: a computer-linked quantitative analysis. Anat. Embryol. (Berl.) 1985;171:339–344. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

