The Berg-Purcell limit revisited
- PMID: 24560000
- PMCID: PMC3945014
- DOI: 10.1016/j.bpj.2013.12.030
The Berg-Purcell limit revisited
Abstract
Biological systems often have to measure extremely low concentrations of chemicals with high precision. When dealing with such small numbers of molecules, the inevitable randomness of physical transport processes and binding reactions will limit the precision with which measurements can be made. An important question is what the lower bound on the noise would be in such measurements. Using the theory of diffusion-influenced reactions, we derive an analytical expression for the precision of concentration estimates that are obtained by monitoring the state of a receptor to which a diffusing ligand can bind. The variance in the estimate consists of two terms, one resulting from the intrinsic binding kinetics and the other from the diffusive arrival of ligand at the receptor. The latter term is identical to the fundamental limit derived by Berg and Purcell (Biophys. J., 1977), but disagrees with a more recent expression by Bialek and Setayeshgar. Comparing the theoretical predictions against results from particle-based simulations confirms the accuracy of the resulting expression and reaffirms the fundamental limit established by Berg and Purcell.
Copyright © 2014 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures
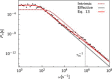

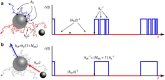
Comment in
-
How accurately can a single receptor measure ligand concentrations?Biophys J. 2014 Feb 18;106(4):778-9. doi: 10.1016/j.bpj.2014.01.010. Biophys J. 2014. PMID: 24559980 Free PMC article. No abstract available.
Similar articles
-
Revising Berg-Purcell for finite receptor kinetics.Biophys J. 2021 Jun 1;120(11):2237-2248. doi: 10.1016/j.bpj.2021.03.021. Epub 2021 Mar 29. Biophys J. 2021. PMID: 33794148 Free PMC article.
-
Cooperativity, sensitivity, and noise in biochemical signaling.Phys Rev Lett. 2008 Jun 27;100(25):258101. doi: 10.1103/PhysRevLett.100.258101. Epub 2008 Jun 23. Phys Rev Lett. 2008. PMID: 18643705
-
Maximum likelihood and the single receptor.Phys Rev Lett. 2009 Oct 9;103(15):158101. doi: 10.1103/PhysRevLett.103.158101. Epub 2009 Oct 7. Phys Rev Lett. 2009. PMID: 19905667
-
Thermodynamic parameters of ligand-receptor interactions: computation and error margins.J Recept Signal Transduct Res. 1997 Jan-May;17(1-3):495-510. doi: 10.3109/10799899709036623. J Recept Signal Transduct Res. 1997. PMID: 9029510 Review.
-
Kinetics of receptor-ligand interactions in immune responses.Cell Mol Immunol. 2006 Apr;3(2):79-86. Cell Mol Immunol. 2006. PMID: 16696894 Review.
Cited by
-
E. coli do not count single molecules.bioRxiv [Preprint]. 2024 Jul 13:2024.07.09.602750. doi: 10.1101/2024.07.09.602750. bioRxiv. 2024. PMID: 39026702 Free PMC article. Preprint.
-
Trading bits in the readout from a genetic network.Proc Natl Acad Sci U S A. 2021 Nov 16;118(46):e2109011118. doi: 10.1073/pnas.2109011118. Proc Natl Acad Sci U S A. 2021. PMID: 34772813 Free PMC article.
-
Know the Single-Receptor Sensing Limit? Think Again.J Stat Phys. 2016;162:1353-1364. doi: 10.1007/s10955-015-1412-9. Epub 2015 Nov 23. J Stat Phys. 2016. PMID: 26941467 Free PMC article.
-
How input noise limits biochemical sensing in ultrasensitive systems.Phys Rev E Stat Nonlin Soft Matter Phys. 2014 Sep;90(3):032702. doi: 10.1103/PhysRevE.90.032702. Epub 2014 Sep 5. Phys Rev E Stat Nonlin Soft Matter Phys. 2014. PMID: 25314468 Free PMC article.
-
Testing the limits of gradient sensing.PLoS Comput Biol. 2017 Feb 16;13(2):e1005386. doi: 10.1371/journal.pcbi.1005386. eCollection 2017 Feb. PLoS Comput Biol. 2017. PMID: 28207738 Free PMC article.
References
-
- Rieke F., Baylor D. Single-photon detection by rod cells of the retina. Rev. Mod. Phys. 1998;70:1027–1036.
-
- Boeckh J., Kaissling K.-E., Schneider D. Insect olfactory receptors. Cold Spring Harb. Symp. Quant. Biol. 1965;30:263–280. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

