Singular perturbation theory for predicting extravasation of Brownian particles

Abstract

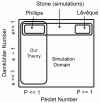
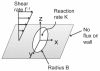
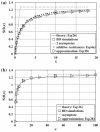
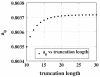
Motivated by recent studies on tumor treatments using the drug delivery of nanoparticles, we provide a singular perturbation theory and perform Brownian dynamics simulations to quantify the extravasation rate of Brownian particles in a shear flow over a circular pore with a lumped mass transfer resistance. The analytic theory we present is an expansion in the limit of a vanishing Péclet number (P), which is the ratio of convective fluxes to diffusive fluxes on the length scale of the pore. We state the concentration of particles near the pore and the extravasation rate (Sherwood number) to O(P^1/2). This model improves upon previous studies because the results are valid for all values of the particle mass transfer coefficient across the pore, as modeled by the Damköhler number (κ), which is the ratio of the reaction rate to the diffusive mass transfer rate at the boundary. Previous studies focused on the adsorption-dominated regime (i.e., κ → ∞). Specifically, our work provides a theoretical basis and an interpolation-based approximate method for calculating the Sherwood number (a measure of the extravasation rate) for the case of finite resistance [κ ~ O(1)] at small Péclet numbers, which are physiologically important in the extravasation of nanoparticles. We compare the predictions of our theory and an approximate method to Brownian dynamics simulations with reflection-reaction boundary conditions as modeled by κ. They are found to agree well at small P and for the κ ≪ 1 and κ ≫ 1 asymptotic limits representing the diffusion-dominated and adsorption-dominated regimes, respectively. Although this model neglects the finite size effects of the particles, it provides an important first step toward understanding the physics of extravasation in the tumor vasculature.

Keywords: Brownian dynamics; Extravasation; Law of additive resistances; Singular perturbation.

Fig. 1

Simulation domain of κ versus P, with the region for which the present theory is developed as shown. Previous work is done only in the adsorption-dominated regime (Phillips [6], Stone [8], Lévêque [9])

Fig. 2

Schematic of our model. The axes are fixed with the origin at the center of the pore embedded in the flat plate with shear flow on it

Fig. 3

Values of a₀, i.e., 2S(P = 0, κ)/π, from Eqs. (14a, b) are plotted for the entire range of κ. The expression resulting from the law of additive resistances (Eq. 4a) and the approximation from Eq. (27) are also plotted for comparison. a a₀ plotted for κ ≪ 1 and κ ~ O(1), along with the two asymptotes. b a₀ plotted for κ ≫ 1 and κ ~ O(1)

Fig. 4

Schematic of simulation domain indicating various coordinate directions and corresponding boundary conditions, along with pore on floor

Fig. 5

Singular perturbation theory (Eq. 26), simulation values, the law of additive resistances (Eq. 4a), and the approximation from Eq. (28) for the extravasation rate at P = 0 for 0 ≤ κ ≤ 100, along with the two asymptotes at the extremes of the domain. a κ ≪ 1 and κ ~ 1. b κ ~ 1 and κ ≫ 1

Fig. 6

Theory (Eq. (26)), approximation (Eq. 28), and Brownian dynamics simulation values of S at P = 0.3 for 0 ≤ κ ≤ 110. a κ ≪ 1 and κ ~ 1. b κ ~ 1 and κ ≫ 1

Fig. 7

Theory (Eq. 26), approximation (Eq. 28), and Brownian dynamics simulation values of S at P = 2 for 0 ≤ κ ≤ 110. a κ ≪ 1 and κ ~ 1. b κ ~ 1 and κ ≫ 1

Fig. 8

Theory (Eq. 26) (dashed), approximation (Eq. 28) (triangles), and Brownian dynamics simulation (boxes) extravasation rates plotted for P ranging from 0 to 100 and κ ≤ 1. a κ = 1. b κ = 0.5

Fig. 9

Theory (Eq. 26) (dashed), approximation (Eq. 28) (triangles), and Brownian dynamics simulation (connected boxes) extravasation rates plotted for P ranging from 0 to 100 and κ > 1. Graetz–Lévêque asymptote (solid line) plotted for κ = 300. a κ = 5. b κ = 10. c κ = 100. d κ = 300.

Fig. 10

Variation of a₀ with truncation length in Eq. (14a, 14b) for κ = 300