A unified model of heading and path perception in primate MSTd

Abstract

Self-motion, steering, and obstacle avoidance during navigation in the real world require humans to travel along curved paths. Many perceptual models have been proposed that focus on heading, which specifies the direction of travel along straight paths, but not on path curvature, which humans accurately perceive and is critical to everyday locomotion. In primates, including humans, dorsal medial superior temporal area (MSTd) has been implicated in heading perception. However, the majority of MSTd neurons respond optimally to spiral patterns, rather than to the radial expansion patterns associated with heading. No existing theory of curved path perception explains the neural mechanisms by which humans accurately assess path and no functional role for spiral-tuned cells has yet been proposed. Here we present a computational model that demonstrates how the continuum of observed cells (radial to circular) in MSTd can simultaneously code curvature and heading across the neural population. Curvature is encoded through the spirality of the most active cell, and heading is encoded through the visuotopic location of the center of the most active cell's receptive field. Model curvature and heading errors fit those made by humans. Our model challenges the view that the function of MSTd is heading estimation, based on our analysis we claim that it is primarily concerned with trajectory estimation and the simultaneous representation of both curvature and heading. In our model, temporal dynamics afford time-history in the neural representation of optic flow, which may modulate its structure. This has far-reaching implications for the interpretation of studies that assume that optic flow is, and should be, represented as an instantaneous vector field. Our results suggest that spiral motion patterns that emerge in spatio-temporal optic flow are essential for guiding self-motion along complex trajectories, and that cells in MSTd are specifically tuned to extract complex trajectory estimation from flow.

Figure 1. Exemplar first-order optic flow fields.

(a) Radially expanding optic flow experienced by an observer traveling along a straight path on a ground plane. The optic flow contains the focus of expansion (FoE) singularity on the horizon, which indicates the heading direction. (b) Movement of an observer along a straight path, as in (a), but with a constant amount of rotation added to the first-order optic flow (simulated rotation condition). Human subjects that view displays with simulated rotation report traveling along a circular path. (c) First-order optic flow experienced by an observer traveling on a circular path whose gaze is along heading or tangent to the circular path.

Figure 2. Experimental paradigm and sample optic flow fields from Froehler and Duffy, who report the existence of path selective neurons in MSTd .

A monkey seated in a sled traveled CCW (a) or CW (c) along a circular track while maintaining gaze on the distal wall of luminous dots. The body, head, and eye did not rotate so that the monkey always directly faced the distal wall. The monkey therefore experienced radially expanding or contracting optic flow without sources of rotation. (b,d) Instantaneous optic flow experienced by the monkey at different locations along the circular track. 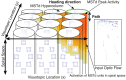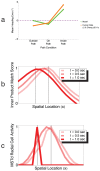In (b) at , the monkey views a radially expanding optic flow while moving CCW when the heading direction is straight ahead, which is the same as the optic flow viewed CW on the other side of the circle. Between and , the FoE drifts rightward until at it is out of view. At , the monkey experiences radial contraction.

Figure 3. Spiral space continuum of motion patterns employed in electrophysiological studies to probe cell selectivity to spiral motion.

Sensitivity to radial expansion and center motion is tested by the left and right ends of the continuum, respectively. Spiral patterns exist in between as an interpolation between the radial and center patterns. The spiral space also contains contracting spirals and those with CCW orientations (not shown).

Figure 4. Schematic depiction of the model coding of path curvature and heading in MSTd.

Neurons in a model MSTd hypercolumn possess selectivities across a spiral space spanning CW, CCW, radial expansion, radial contraction, and center motion patterns. The length and width dimensions of the schematic MSTd selectivity volume correspond to neurons with 2D visuotopic tuning. Therefore, at every position in the visual field, there is a model MSTd hypercolumn with a full set of units tuned to radial, spiral, and center optic flow patterns. For example, the hypercolumn on the top left corresponds to MSTd units with receptive fields centered on the top left portion of the visual field, which have focus of expansion or center of motion tuning in that location. Travel along a circular path elicits a distribution of activity within the MSTd volume (overlaid heat map). The position of the activity peak across the volume in the spiral space (depth) dimension corresponds to the model path curvature estimate, and the 2D position of the peak in the spatial dimensions (length and width) indicates the estimated heading direction.

Figure 5. Diagram of model V1-MT-MSTd.

First-order local motion is computed in model V1. Model MT receives projections and spatially pools motion signals from model V1. A extra-retinal eye velocity gain field acts on the afferent signals from model MT in MSTd, which compensates for rotation introduced by pursuit eye movements proportional to the eye movement speed in the direction opposite that of the eye movement. A template match occurs in model MSTd, whereby the similarity is assessed between the afferent motion signal and motion field templates sampled in spiral space. A distance-dependent weighting exponentially discounts vector matches by distance from the template singularity. Finally, neurons selective to different spiral patterns, expansion and contraction, CW and CCW orientations, and 2D visuotopic location compete.

Figure 6. Observer gaze conditions during travel along a circular path tested in the model from Li and Cheng .

The gaze in each condition is “simulated” within the computer display because human subjects in the experiments of Li and Cheng maintained fixation throughout the trial. We also tested the model on analogous conditions with pursuit eye movements (see Figure 8). (a) Z-axis condition. The observer maintains a fixed body, head, and eye orientation, in the direction of the ‘Z axis’, during travel along the circular path. The optic flow field at every instant is radially expansive, and over time the FoE drifts horizontally. (b) Outside path condition. 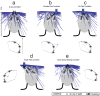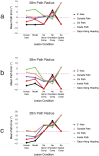Observer gaze was maintained on a target positioned outside the path. (c) On path condition. The observer maintained gaze on a target on the future path positioned from the initial heading. (d) Inside path condition. Observer gaze was maintained on a target positioned inside the path. (e) Gaze along heading condition. Observer gaze is always tangent to the circular path, which is most often the case during human locomotion. Human subjects in the experiments of Li and Cheng underestimated path curvature in the Z axis, outside path, and on path conditions, overestimated path curvature in the inside path condition, and yielded low error in their judgments in the gaze along heading condition.

Figure 7. Path errors obtained by the model in the five gaze conditions.

(a) Path error averaged across circular path radius. Positive and negative path errors indicate overestimations and underestimations of path curvature, respectively, and zero path error signifies veridical performance. Both humans and the model underestimated path curvature in the Z axis, outside path, and on path conditions, overestimated path curvature in the inside path condition, and elicited near veridical performance in the gaze along heading condition. 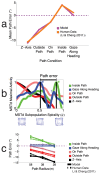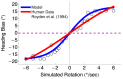(b) Model MSTd activity across spiral pattern selectivity space during an exemplar trial with a path radius for the five gaze conditions. The location of each peak across the spiral continuum determines the model estimate of path curvature. For example, in the Z-axis condition (black), the MSTd activity peak occurs in the subpopulation sensitive to radial expansion (), and therefore the model indicates zero path curvature (straight path). (c) Model path errors (solid lines) compared to human data from Li and Cheng (replotted, dashed lines) in the five gaze conditions as a function of path curvature . Model path errors were in good agreement in all gaze conditions with those based on human judgments (), and path error decreased linearly () with path curvature. Error bars correspond to standard error of the mean (SEM).

Figure 8. Model path error in conditions that involve smooth pursuit eye movements.

The optic flow that appears on the observer retinal during smooth pursuit of a horizontally moving target is identical in the orientation along heading and orientation along Z-axis conditions. The orientation along heading condition is similar to the gaze along heading condition, except the observer tracks a target that moves in the direction opposite of the path curvature. The orientation along Z-axis condition is similar to the Z-axis condition, except the observer tracks a target that moves in the same direction of the path curvature. Similar to human subjects, the model yields low path errors for all the path radius conditions because model gain fields compensate in the direction opposite that of the eye movements. The model increasingly underestimates path curvature in the orientation along Z-axis condition, similar to humans.

Figure 9. Heading errors produced by the model during travel along a circular path.

Positive and negative heading errors indicate bias in heading judgments in the direction of and the direction opposite to the path curvature, respectively. The model and humans produced small negative heading errors in the on path condition, and more substantial positive bias in the inside path condition. The model yielded veridical heading performance in the outside path condition, which occurred because the model is not sensitive enough to differences in the optic flow in the outside path and Z-axis conditions. Heading bias in the model is preserved over time without (b) and with (c) competition in MSTd.

Figure 10. Heading bias yielded by the model in the simulated rotation condition with rotation rates between .

When human subjects fixate on optic flow displays wherein an observer moves along a straight path with rotation, humans make large heading errors in the direction of the simulated rotation and report the perception of travel along a curved path. The model (blue) produced the same sigmoidal pattern of heading bias as human subjects (red). Both sets of data points were fit well with a hyperbolic tangent function. The similarity between model and human heading bias, suggests the model mechanisms can explain the curved path percept reported by human subjects.

Figure 11. The impact lesions to model MSTd have on path error.

The mean path errors for human subjects and the model from Figure 7 are plotted on the two leftmost data columns for (a), (b), (c) radius paths. Lesions were introduced in the model MSTd connectivity by zeroing out competitive interactions in spiral space, across spiral orientation, and across 2D space between neurons in MSTd (see Eq. 6). Lesions had a detrimental impact on model performance, and path curvature estimates no longer mapped onto human judgments. The three competitive interactions in model MSTd were necessary to obtain our results.

Figure 12. Robustness in model path curvature estimates for scenes containing –.

The deviation in path errors from those shown in Figure 7 are plotted for path radii of (a), (b), and (c), respectively. Deviations in path error were modest, with mean errors falling within of those depicted in Figure 7. There were only small deviations in any condition when the scene contained at least .

Figure 13. Model simulation of the experiment of Froehler and Duffy .

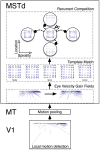
(a) Responses of the maximally-active model MSTd subpopulations in spiral space as a function of the angular rotation rate (i.e. how fast the circular path is traversed per unit of time). When the angular rotation rate matched that used by Froehler and Duffy (, dark orange), model MSTd neurons most sensitive to spiral patterns were most active. This also occurred when for larger angular rotation rates (). When the angular rotation was set to a comparable rate to that used in the Z-axis condition (), model MSTd neurons most sensitive to radial expansion elicited the maximal activation. (b) Simplified model mechanisms that explain why neurons that are sensitive to spirals produced the peak activity in spiral space in the simulation of the Froehler and Duffy experiment, but did not in the simulation of the Z-axis condition. Consider the first-order optic flow ( and ) at two times ( and ) during the circular path traversal (top row). Template matching in the model is inversely weighted by distance to the FoE or CoM (second row). The third row shows the optimal templates inversely weighted by distance ( and ). Because model MSTd dynamically integrates afferent signals from model MT, activation due to the input at influences the activation due to the input at . Temporal accumulation in the model can be approximated by considering , which temporally blends the two weighted fields. This yields a spiral field (bottom row), and explains why model MSTd neurons sensitive to spiral patterns are most active when the angular rotation rate about the circular path is sufficiently large.