Stability indicators in network reconstruction
- PMID: 24587057
- PMCID: PMC3937450
- DOI: 10.1371/journal.pone.0089815
Stability indicators in network reconstruction
Abstract
The number of available algorithms to infer a biological network from a dataset of high-throughput measurements is overwhelming and keeps growing. However, evaluating their performance is unfeasible unless a 'gold standard' is available to measure how close the reconstructed network is to the ground truth. One measure of this is the stability of these predictions to data resampling approaches. We introduce NetSI, a family of Network Stability Indicators, to assess quantitatively the stability of a reconstructed network in terms of inference variability due to data subsampling. In order to evaluate network stability, the main NetSI methods use a global/local network metric in combination with a resampling (bootstrap or cross-validation) procedure. In addition, we provide two normalized variability scores over data resampling to measure edge weight stability and node degree stability, and then introduce a stability ranking for edges and nodes. A complete implementation of the NetSI indicators, including the Hamming-Ipsen-Mikhailov (HIM) network distance adopted in this paper is available with the R package nettools. We demonstrate the use of the NetSI family by measuring network stability on four datasets against alternative network reconstruction methods. First, the effect of sample size on stability of inferred networks is studied in a gold standard framework on yeast-like data from the Gene Net Weaver simulator. We also consider the impact of varying modularity on a set of structurally different networks (50 nodes, from 2 to 10 modules), and then of complex feature covariance structure, showing the different behaviours of standard reconstruction methods based on Pearson correlation, Maximum Information Coefficient (MIC) and False Discovery Rate (FDR) strategy. Finally, we demonstrate a strong combined effect of different reconstruction methods and phenotype subgroups on a hepatocellular carcinoma miRNA microarray dataset (240 subjects), and we validate the analysis on a second dataset (166 subjects) with good reproducibility.
Conflict of interest statement
Figures
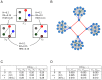
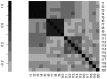
 , as defined in Subsection Stability is modularity invariant.
, as defined in Subsection Stability is modularity invariant.  : network
: network  without the four red links.
without the four red links.  : network
: network  without green links.
without green links.  : network
: network  without blue links. (C) The mutual differences between the pairs of networks in (A),
without blue links. (C) The mutual differences between the pairs of networks in (A),  and
and  . (D)
. (D)  ,
,  ,
,  . In both cases they have the same Hamming distance but different spectral structure, thus resulting in different Ipsen-Mikhailov distances.
. In both cases they have the same Hamming distance but different spectral structure, thus resulting in different Ipsen-Mikhailov distances.

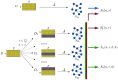
 , the network
, the network  is first reconstructed from the whole dataset
is first reconstructed from the whole dataset  with
with  samples and
samples and  features (nodes). Given two integers
features (nodes). Given two integers  , a set of
, a set of  datasets
datasets  is generated by choosing for each
is generated by choosing for each  a subset of
a subset of  samples from
samples from  , and the corresponding networks
, and the corresponding networks  are inferred by
are inferred by  . Finally, the four indicators
. Finally, the four indicators  ,
,  ,
,  and
and  are computed according to their definition.
are computed according to their definition.


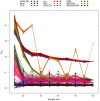



 corresponds to feature
corresponds to feature  , node size is proportional to node degree and link colors identify different classes of link weights.
, node size is proportional to node degree and link colors identify different classes of link weights.

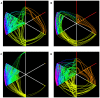
 pointing upwards collects all the nodes with (unweighted) degree 0 or 1;
pointing upwards collects all the nodes with (unweighted) degree 0 or 1;  , the next axis moving clockwise, is a copy of
, the next axis moving clockwise, is a copy of  ; the following two axes include all nodes with degree 2, while on the remaining two axes lie all nodes with degree 3 or more. Different colors indicate different degree. Nodes on axes are ranked by degree. Lines between two consecutive axes show the network's edges and edge color is inherited by the node with smaller degree. Note the absence of links between nodes of degreee 1 and 2 in the FT case, and the smaller amount of connections between higher degree nodes in the MnT case with respect to the other three cases.
; the following two axes include all nodes with degree 2, while on the remaining two axes lie all nodes with degree 3 or more. Different colors indicate different degree. Nodes on axes are ranked by degree. Lines between two consecutive axes show the network's edges and edge color is inherited by the node with smaller degree. Note the absence of links between nodes of degreee 1 and 2 in the FT case, and the smaller amount of connections between higher degree nodes in the MnT case with respect to the other three cases.

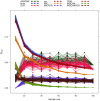
 -fold cross validation for
-fold cross validation for  set to 2 (
set to 2 ( ), 4 (
), 4 ( ) and 10 (
) and 10 ( ) respectively.
) respectively.References
-
- Zhang B, Horvath S (2005) A General Framework for Weighted Gene Co-Expression Network Analysis. Statistical Applications in Genetics and Molecular Biology 4: Article 17. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

