Interplay between chain stiffness and excluded volume of semiflexible polymers confined in nanochannels

Abstract

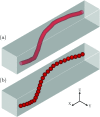
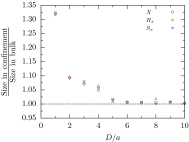
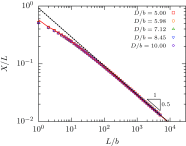
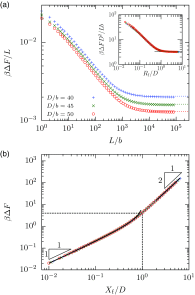
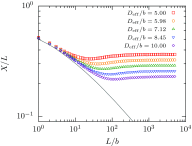
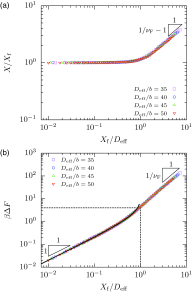
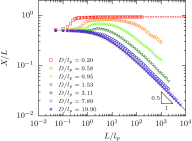
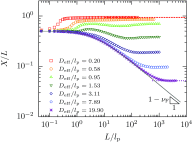
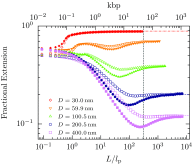
The properties of channel-confined semiflexible polymers are determined by a complicated interplay of chain stiffness and excluded volume effects. Using Pruned-Enriched Rosenbluth Method (PERM) simulations, we study the equilibrium properties of channel-confined polymers by systematically controlling chain stiffness and excluded volume. Our calculations of chain extension and confinement free energy for freely jointed chains with and without excluded volume show excellent agreement with theoretical predictions. For ideal wormlike chains, the extension is seen to crossover from Odijk behavior in strong confinement to zero-stretching, bulk-like behavior in weak confinement. In contrast, for self-avoiding wormlike chains, we always observe that the linear scaling of the extension with the contour length is valid in the long-chain limit irrespective of the regime of confinement, owing to the coexistence of stiffness and excluded volume effects. We further propose that the long-chain limit for the extension corresponds to chain lengths wherein the projection of the end-to-end distance along the axis of the channel is nearly equal to the mean span parallel to the axis. For DNA in nanochannels, this limit was identified using PERM simulations out to molecular weights of more than 1 megabase pairs; the molecular weight of λ-DNA is found to exhibit nearly asymptotic fractional extension for channels sizes used commonly in experiments.

Figure 1

(a) A WLC with contour length L, persistence length l_p, and width w confined in a square channel of size D. (b) Representation of the same chain in our DWLC model. After discretization, the bond length a is set equal to the value of the width w.

Figure 2

Mean span (X), x-projection of the end-to-end distance (R_x) and x − x component of the gyration tensor (S_x), normalized by the corresponding quantities in free solution for an ideal FJC, plotted against D/a. The dashed line at unity is the expected result in the absence of discretization error. All data points show simulation results for a contour length L/a = 5000.

Figure 3

Average fractional extension as a function of contour length for IFJCs confined in square channels of various sizes. Most data points are not visible as they overlap each other exactly. The red line denotes the theoretical prediction in Eq. 13 for IFJCs in free solution. The dashed line is the result for the mean span in the long-chain limit given by $X=\sqrt{8Lb/3\pi }$. All results show a scaling of X ∼ L^0.5 in the long-chain limit, as expected.

Figure 4

(a) Free energy of ideal FJCs in 3 square channels of different sizes. The free energy values asymptote to the value given by Eq. 15 (dashed lines)., In the inset, the free energy values are shown to reach asymptotic scaling for all 3 channels when R_f ≈ D. The dashed line signifies the theoretically expected limit, π²/3. (b) Free energy data for the 3 channels fall on a universal curve as per scaling theory, with an asymptotic scaling ΔF ∼ (X_f/D)² for X_f ≫ D. The dashed lines show that the free energy of confinement is approximately 4k_BT for X_f/D = 1. The solid black lines show theoretical predictions: Eq. 17 for X_f/D ≲ 1, and Eq. 15 for X_f/D ≳ 1. A scaling of ΔF ∼ (X_f/D)¹ is also seen for X_f ≪ D.

Figure 5

Fractional extension of RFJCs (a = w = b) confined in channels with same D_eff values as in Fig. 3. The gray line corresponds to simulation results of a RFJC in free solution.

Figure 6

(a) Ratio of extension in confinement with extension in the bulk versus ratio of the free-solution mean span with the channel size for 4 channels. (b) Confinement free energy for the chains under the same conditions. The dashed lines show that the confinement free energy is $\mathcal{O}\left(k_{\text{B}}T\right)$ when X_f/D_eff = 1. The prediction in Eq. 22 is shown as a solid black line. Also shown is the scaling, βΔF ∼ X_f/D_eff, in the weak confinement regime. Notice the scaling of both properties in the long-chain limit: $X/X_{\text{f}}\sim {\left(X_{\text{f}}/D_{\text{eff}}\right)}^{1/{\nu }_{\text{F}}-1}$, and $\Delta F\sim {\left(X_{\text{f}}/D_{\text{eff}}\right)}^{1/{\nu }_{\text{F}}}$. The data shown here correspond to RFJCs of contour length L ranging from L = b to L = 5000b.

Figure 7

Fractional extension of IWLCs with l_p/a = 20 versus contour length for various channel sizes. The gray line shows simulation results for fractional extension of the chain in free solution with an expected slope of −0.5 in the long-chain limit. The red dashed line corresponds to the prediction in the Odijk regime given by Eq. 23.

Figure 8

Fractional extension of RWLCs with l_p/a = 20 versus contour length for the same D_eff values as in Fig. 7. The gray line depicts the fractional extension for the chain in free solution with an expected slope of −(1 − ν_F) ≃ − 0.42 in the long-chain limit. Our results agree with predicted extension in the Odijk regime (red dashed line) and prior results for the long-chain limit in the de Gennes regime (purple dotted line). However, most other curves fall in the transition regime.

Figure 9

Mean span X (unfilled symbols) and projection of the end-to-end distance on the axis of the channel R_x (filled symbols) normalized by the contour length for confined, undyed DNA in a high ionic strength buffer. Note that the x axis at the bottom indicates the number of persistence lengths of the chain and the x axis at the top denotes the length of DNA in units of kilobase pairs. The red dashed-dotted line corresponds to the asymptotic fractional extension in the Odijk regime. The dashed lines corresponding to the two biggest channels show the empirical fit obtained by for the long-chain limit in the de Gennes regime. The molecular weight of λ-DNA is shown as a vertical gray dashed line.