Recasting the theory of mosquito-borne pathogen transmission dynamics and control
- PMID: 24591453
- PMCID: PMC3952634
- DOI: 10.1093/trstmh/tru026
Recasting the theory of mosquito-borne pathogen transmission dynamics and control
Abstract
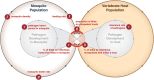
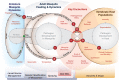
Mosquito-borne diseases pose some of the greatest challenges in public health, especially in tropical and sub-tropical regions of the world. Efforts to control these diseases have been underpinned by a theoretical framework developed for malaria by Ross and Macdonald, including models, metrics for measuring transmission, and theory of control that identifies key vulnerabilities in the transmission cycle. That framework, especially Macdonald's formula for R0 and its entomological derivative, vectorial capacity, are now used to study dynamics and design interventions for many mosquito-borne diseases. A systematic review of 388 models published between 1970 and 2010 found that the vast majority adopted the Ross-Macdonald assumption of homogeneous transmission in a well-mixed population. Studies comparing models and data question these assumptions and point to the capacity to model heterogeneous, focal transmission as the most important but relatively unexplored component in current theory. Fine-scale heterogeneity causes transmission dynamics to be nonlinear, and poses problems for modeling, epidemiology and measurement. Novel mathematical approaches show how heterogeneity arises from the biology and the landscape on which the processes of mosquito biting and pathogen transmission unfold. Emerging theory focuses attention on the ecological and social context for mosquito blood feeding, the movement of both hosts and mosquitoes, and the relevant spatial scales for measuring transmission and for modeling dynamics and control.
Keywords: Dengue; Filariasis; Malaria; Mosquito-borne pathogen transmission; Vector control; West Nile virus.
Figures

References
-
- Murray CJ, Vos T, Lozano R, et al. Disability-adjusted life years (DALYs) for 291 diseases and injuries in 21 regions, 1990–2010: a systematic analysis for the Global Burden of Disease Study 2010. Lancet. 2012;380:2197–223. 10.1016/S0140-6736(12)61689-4. - DOI - PubMed
-
- Cibulskis RE, Aregawi M, Williams R, et al. Worldwide incidence of malaria in 2009: estimates, time trends, and a critique of methods. PLoS Med. 2011;8(12) e1001142 10.1371/journal.pmed.1001142. - DOI - PMC - PubMed
-
- Hay SI, Okiro EA, Gething PW, et al. Estimating the global clinical burden of Plasmodium falciparum malaria in 2007. PLoS Med. 2010;7(6) e1000290 10.1371/journal.pmed.1000290. - DOI - PMC - PubMed
-
- Murray CJ, Rosenfeld LC, Lim SS, et al. Global malaria mortality between 1980 and 2010: a systematic analysis. Lancet. 2012;379:413–31. 10.1016/S0140-6736(12)60034-8. - DOI - PubMed
-
- WHO. Geneva: World Health Organization; 2010. World Malaria Report.
Publication types
MeSH terms
Grants and funding
- R01 AI069341/AI/NIAID NIH HHS/United States
- 095066/WT_/Wellcome Trust/United Kingdom
- U01 GM070708/GM/NIGMS NIH HHS/United States
- DP1 OD003874/OD/NIH HHS/United States
- R01-GM08322/GM/NIGMS NIH HHS/United States
- 5 U01 EH000418/EH/NCEH CDC HHS/United States
- K00669X/MRC_/Medical Research Council/United Kingdom
- U01GM070708/GM/NIGMS NIH HHS/United States
- U19AI089674/AI/NIAID NIH HHS/United States
- MR/K00669X/1/MRC_/Medical Research Council/United Kingdom
- U01 EH000418/EH/NCEH CDC HHS/United States
- R01 AI069387-01A1/AI/NIAID NIH HHS/United States
- DP1OD003874/OD/NIH HHS/United States
- R01-AI091980/AI/NIAID NIH HHS/United States
- T32 GM008322/GM/NIGMS NIH HHS/United States
- R01-AI069341/AI/NIAID NIH HHS/United States
- R01 AI069387/AI/NIAID NIH HHS/United States
- R01 AI091980/AI/NIAID NIH HHS/United States
- U19 AI089674/AI/NIAID NIH HHS/United States
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

