Energy losses of nanomechanical resonators induced by atomic force microscopy-controlled mechanical impedance mismatching
- PMID: 24594876
- PMCID: PMC3959189
- DOI: 10.1038/ncomms4345
Energy losses of nanomechanical resonators induced by atomic force microscopy-controlled mechanical impedance mismatching
Abstract
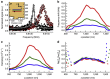
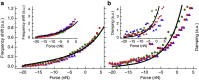
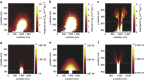
Clamping losses are a widely discussed damping mechanism in nanoelectromechanical systems, limiting the performance of these devices. Here we present a method to investigate this dissipation channel. Using an atomic force microscope tip as a local perturbation in the clamping region of a nanoelectromechanical resonator, we increase the energy loss of its flexural modes by at least one order of magnitude. We explain this by a transfer of vibrational energy into the cantilever, which is theoretically described by a reduced mechanical impedance mismatch between the resonator and its environment. A theoretical model for this mismatch, in conjunction with finite element simulations of the evanescent strain field of the mechanical modes in the clamping region, allows us to quantitatively analyse data on position and force dependence of the tip-induced damping. Our experiments yield insights into the damping of nanoelectromechanical systems with the prospect of engineering the energy exchange in resonator networks.
Figures
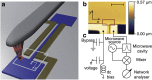
 for the out-of-plane mode for a clamp with no undercut. (e) The same with a realistic undercut of the silicon nitride pedestal of 500 nm. (f) Simulated
for the out-of-plane mode for a clamp with no undercut. (e) The same with a realistic undercut of the silicon nitride pedestal of 500 nm. (f) Simulated  for the fundamental in-plane mode with 500 nm undercut.
for the fundamental in-plane mode with 500 nm undercut.References
-
- Ekinci K. L. & Roukes M. L. Nanoelectromechanical systems. Rev. Sci. Instrum. 76, 061101 (2005).
-
- Chan J., Safavi-Naeini A. H., Hill J. T., Meenehan S. & Painter O. Optimized optomechanical crystal cavity with acoustic radiation shield. Appl. Phys. Lett. 101, 081115 (2012).
-
- Mamin H. J. & Rugar D. Sub-attonewton force detection at millikelvin temperatures. Appl. Phys. Lett. 79, 3358 (2001).
-
- Knobel R. G. & Cleland A. N. Nanometre-scale displacement sensing using a single electron transistor. Nature 424, 291–293 (2003). - PubMed
-
- Rugar D., Budakian R., Mamin H. J. & Chui B. W. Single spin detection by magnetic resonance force microscopy. Nature 430, 329–332 (2004). - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

