The effect of linkage on establishment and survival of locally beneficial mutations

Abstract

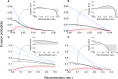
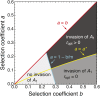
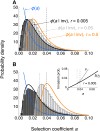
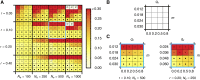
We study invasion and survival of weakly beneficial mutations arising in linkage to an established migration-selection polymorphism. Our focus is on a continent-island model of migration, with selection at two biallelic loci for adaptation to the island environment. Combining branching and diffusion processes, we provide the theoretical basis for understanding the evolution of islands of divergence, the genetic architecture of locally adaptive traits, and the importance of so-called "divergence hitchhiking" relative to other mechanisms, such as "genomic hitchhiking", chromosomal inversions, or translocations. We derive approximations to the invasion probability and the extinction time of a de novo mutation. Interestingly, the invasion probability is maximized at a nonzero recombination rate if the focal mutation is sufficiently beneficial. If a proportion of migrants carries a beneficial background allele, the mutation is less likely to become established. Linked selection may increase the survival time by several orders of magnitude. By altering the timescale of stochastic loss, it can therefore affect the dynamics at the focal site to an extent that is of evolutionary importance, especially in small populations. We derive an effective migration rate experienced by the weakly beneficial mutation, which accounts for the reduction in gene flow imposed by linked selection. Using the concept of the effective migration rate, we also quantify the long-term effects on neutral variation embedded in a genome with arbitrarily many sites under selection. Patterns of neutral diversity change qualitatively and quantitatively as the position of the neutral locus is moved along the chromosome. This will be useful for population-genomic inference. Our results strengthen the emerging view that physically linked selection is biologically relevant if linkage is tight or if selection at the background locus is strong.

Keywords: adaptive divergence; establishment; gene flow; linked selection; local adaptation.

Figure 1

Invasion probability of A₁ as a function of the recombination rate for a monomorphic continent. (A and B) Weighted average invasion probabilitiy $\overline{\pi }$ across the two genetic backgrounds B₁ and B₂ (Equations 2 and 4). For comparison, horizontal dashed lines give 10% of Haldane’s (1927) approximation 2a, valid for m = 0 and r = 0.5. (B) The optimal recombination rate r_opt, defined as the recombination rate at which $\overline{\pi }$ is maximized (red arrow), is nonzero. (C) Same as in B, but in addition to the weighted average, the invasion probabilities of A₁ conditional on initial occurrence on the B₁ or B₂ background are shown in blue or red, respectively. Note the difference in the scale of the vertical axis between B and C. In A–C, curves show exact numerical solutions to the branching process. Dots represent the point estimates across 10⁶ simulations under the branching-process assumptions (see Methods). Error bars span twice the standard error on each side of the point estimates, but are too short to be visible.

Figure 2

Approximation to the invasion probability of A₁ for a monomorphic continent. Invasion probabilities are shown for A₁ initially occurring on the beneficial background B₁ (blue), on the deleterious background B₂ (red), and as a weighted average across backgrounds (black). Analytical approximations assuming a slightly supercritical branching process (dot-dashed curves) and, in addition, weak evolutionary forces (Equation 12; thick dashed curves) are compared to the exact numerical branching-process solution (solid curves). Inset figures show the error of the analytical approximation $\overline{\tilde{\pi }}\left(\zeta \right)$ (thick dashed black curve) relative to $\overline{\pi }$ (solid black curve), $\overline{\tilde{\pi }}\left(\zeta \right)/\overline{\pi }-1.$ (A) a = 0.02, b = 0.04, m = 0.022. (B) a = 0.02, b = 0.04, m = 0.03. (C) a = 0.2, b = 0.4, m = 0.22. (D) a = 0.2, b = 0.4, m = 0.3. As expected, the analytical approximations are very good for weak evolutionary forces (top row), but less so for strong forces (bottom row).

Figure 3

Optimal recombination rate and regions of invasion. The dark shaded area indicates where the optimal recombination rate r is positive (r_opt > 0; cf. Figure 1B). The medium shaded area shows the parameter range for which r_opt = 0 (cf. Figure 1A). Together, these two areas indicate where A₁ can invade via the marginal one-locus migration–selection equilibrium E_B if r is sufficiently small. The light shaded area shows where E_B does not exist and A₁ cannot invade via E_B. The area above a = b is not of interest, as we focus on mutations that are weakly beneficial compared to selection at the background locus (a < b). The critical selection coefficient a^∗ is given in Equation 14 and the migration rate is m = 0.3 (other values of m yield qualitatively similar diagrams). The continent is monomorphic (q_c = 0).

Figure 4

DFE of successfully invading mutations for a monomorphic continent. The DFE of successfully invading mutations was obtained as $\phi \left(a|\text{inv}\right)=\phi \left(\text{inv}|a\right)\phi \left(a\right)/{\displaystyle {\int }_0^{\mathrm{\infty }}\phi \left(\text{inv}|a\right)\phi \left(a\right)da}$, where $\phi \left(\text{inv}|a\right)=\overline{\tilde{\pi }}\left(\xi \right)={\widehat{q}}_{\text{B}}{\tilde{\pi }}_1\left(\xi \right)+\left(1-{\widehat{q}}_{\text{B}}\right){\tilde{\pi }}_2\left(\xi \right),$ with ${\widehat{q}}_{\text{B}}$ and ${\tilde{\pi }}_i\left(\xi \right)$ as in Equations 2 and 12, respectively. The mutational input distribution was assumed to be exponential, φ(a) = λe^−aλ (blue). Vertical lines denote a = m (dotted) and a = b (dashed). Histograms were obtained from simulations under the branching-process assumptions (intermediate shading indicates where histograms overlap). Each represents 2.5 × 10⁴ realizations in which A₁ successfully invaded (see Methods). As a reference, the one-locus model (no linkage) is shown in orange. (A) Relatively weak migration: b = 0.04, m = 0.01. (B) Migration three times stronger: b = 0.04, m = 0.03. In A and B, λ = 100 and $\phi \left(a|\text{inv}\right)$ is shown for a recombination rate of r = 0.005 (black) and r = 0.05 (gray). The inset in B shows why the fit is worse for r = 0.005: in this case, $\overline{\tilde{\pi }}\left(\xi \right)$ underestimates the exact invasion probability $\overline{\pi }$ (Equation 4) for large a.

Figure 5

Diffusion approximation to the sojourn-time density of A₁ under quasi-linkage equilibrium for a monomorphic continent. Comparison of the STD t_2,QLE(p; p₀) (thin black; Equation 7b) to the approximation valid for small p₀, ${\tilde{t}}_{2,\text{QLE}}\left(p;p_0\right)$ (dashed black; Equation 109 in File S1), and the one based on the additional assumption of ρ ≫ max(α, β, μ), ${\tilde{t}}_{2,\text{QLE},\rho \gg 0}\left(p;p_0\right)$ (dotted; Equation 17b). The STD for the one-locus model, ${\tilde{t}}_{2,\text{OLM}}\left(p;p_0\right)$, is shown in orange as a reference. Vertical lines give the deterministic frequency ${\widehat{p}}_{+}$ of A₁ at the fully polymorphic equilibrium (computed in File S7). (A) Weak evolutionary forces relative to genetic drift. (B) As in A, but with half the scaled recombination rate ρ. The assumption of ρ ≫ max(α, β, μ) is violated and hence ${\tilde{t}}_{2,\text{QLE},\rho \gg 0}\left(p;p_0\right)$ is a poor approximation of t_2,QLE(p; p₀). (C) Strong evolutionary forces relative to genetic drift. The STD has a pronounced mode different from p = 0, but ${\tilde{t}}_{2,\text{QLE},\rho \gg 0}\left(p;p_0\right)$ overestimates t_2,QLE(p; p₀) considerably. (D) Strong assymmetry in selection coefficients and moderate migration. As in C, the STD has a pronounced mode different from p = 0, but ${\tilde{t}}_{2,\text{QLE},\rho \gg 0}\left(p;p_0\right)$ now approximates t_2,QLE(p; p₀) better. (E) Recombination 10 times stronger than selection at locus B. (F) As in E, but with recombination 100 times stronger than selection at locus B. In A–F, p₀ = 0.005, which corresponds to an island population of size N = 100 and a single initial copy of A₁.

Figure 6

Relative error of the diffusion approximation to the mean absorption time of A₁. (A) The error of ${\overline{t}}_{\text{QLE}}$ from Equation 8 relative to simulations for various parameter combinations. Squares bounded by thick lines delimit combinations of values of the recombination rate r and the effective population size N_e. Within each of them, values of the migration rate m and the continental frequency q_c of B₁ are as shown in B. No negative relative errors were observed. For better resolution, we truncated values >0.30 (the maximum was 3.396 for N_e = 1000, r = 0.05, m = 0.018, q_c = 0.0). Open (solid) circles indicate that the marginal one-locus equilibrium ${\tilde{E}}_B$ is unstable (stable) and A₁ can (not) be established under deterministic dynamics. Parameter combinations for which simulations were too time consuming are indicated by ∅. Selection coefficients are a = 0.02 and b = 0.04. (C) The left plot corresponds to the square in A that is framed in blue. The right plot shows the fit of the diffusion approximation to simulations conducted with unscaled parameters twice as large and N_e half as large, as on the left side. Scaled parameters are equal on both sides. As expected, the diffusion approximation is worse on the right side. Simulations were as described in Methods. See Table S1 for numerical values.

Figure 7

Mean absorption time of A₁ under quasi-linkage equilibrium relative to the one-locus model (OLM). In panels (A), (B), (D) and (E), thin solid curves show the ratio ${\tilde{\overline{t}}}_{\text{QLE}}/{\tilde{\overline{t}}}_{\text{OLM}}$ and thick dashed curves ${\tilde{\overline{t}}}_{\text{QLE},\rho \gg 0}/{\tilde{\overline{t}}}_{\text{OLM}}$, as a function of the migration rate m. The effective population size N_e increases from light to dark gray, taking values of 100, 250, 500, and 1000. Vertical lines denote the migration rate below which A₁ can invade in the deterministic one-locus (orange) and two-locus (black) model. (A) Recombination is too weak for the assumption ρ ≫ max(α, β, μ) to hold. (B) As in (A), but with recombination four times stronger. (D) Evolutionary forces – other than drift – are ten times stronger than in (B). (E) As in (D), but with recombination ten times stronger. Panels (C) and (F) show the mean absorption time (in multiples of 2N_e) under the one-locus model for the respective row. For m close to 0, numerical procedures are unstable and we truncated the curves. As m converges to 0, ${\tilde{\overline{t}}}_{\text{QLE}}/{\tilde{\overline{t}}}_{\text{OLM}}$ and ${\tilde{\overline{t}}}_{\text{QLE},\rho \gg 0}/{\tilde{\overline{t}}}_{\text{OLM}}$ are expected to approach unity, however.

Figure 8

The effect of linked selection on neutral diversity and population divergence. Shown are top views of the stationary allele frequency distribution on the island for a neutral biallelic locus C linked to two selected sites at (locus A) 20 and (locus B) 60 map units from the left end of the chromosome. Density increases from light blue to yellow (high peaks were truncated for better resolution). Orange and white curves show the expected diversity (heterozygosity H) and population divergence (F_ST) as a function of the position of the neutral site. Solid curves use exact, numerically computed values of the effective migration rate and dashed curves use the approximations given in Equation 23. One map unit (cM) corresponds to r = 0.01 and the effective size of the island population is N_e = 100. The continental frequency n_c of allele C₁ is indicated by a horizontal black line and, from left to right, equal to 0.2, 0.5 and 0.8. (A–C) Relatively strong drift and weak migration compared to selection: α = 4, β = 80, μ = 2. (D–F) Relatively weak drift and migration on the same order of magnitude as selection at locus A: α = 40, β = 800, μ = 48. Note that H is sensitive to n_c, whereas F_ST is not. On top of D and E, allele frequency distributions that result from taking vertical slices at positions indicated by red arrows are shown (15, 59 and 90 cM).