Distinguishing Between Reservoir Exposure and Human-to-Human Transmission for Emerging Pathogens Using Case Onset Data

Abstract

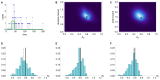
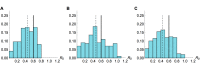
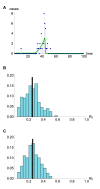
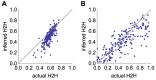
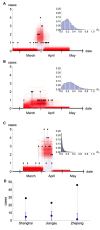
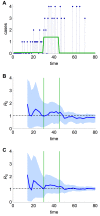
Pathogens such as MERS-CoV, influenza A/H5N1 and influenza A/H7N9 are currently generating sporadic clusters of spillover human cases from animal reservoirs. The lack of a clear human epidemic suggests that the basic reproductive number R0 is below or very close to one for all three infections. However, robust cluster-based estimates for low R0 values are still desirable so as to help prioritise scarce resources between different emerging infections and to detect significant changes between clusters and over time. We developed an inferential transmission model capable of distinguishing the signal of human-to-human transmission from the background noise of direct spillover transmission (e.g. from markets or farms). By simulation, we showed that our approach could obtain unbiased estimates of R0, even when the temporal trend in spillover exposure was not fully known, so long as the serial interval of the infection and the timing of a sudden drop in spillover exposure were known (e.g. day of market closure). Applying our method to data from the three largest outbreaks of influenza A/H7N9 outbreak in China in 2013, we found evidence that human-to-human transmission accounted for 13% (95% credible interval 1%-32%) of cases overall. We estimated R0 for the three clusters to be: 0.19 in Shanghai (0.01-0.49), 0.29 in Jiangsu (0.03-0.73); and 0.03 in Zhejiang (0.00-0.22). If a reliable temporal trend for the spillover hazard could be estimated, for example by implementing widespread routine sampling in sentinel markets, it should be possible to estimate sub-critical values of R0 even more accurately. Should a similar strain emerge with R0>1, these methods could give a real-time indication that sustained transmission is occurring with well-characterised uncertainty.

Keywords: H7N9; Influenza; infectious diseases; statistical inference; zoonoses.

Simulation results with mean serial interval λ=6 days and R₀=0.6.

Results from inference using simulated time series with R₀ =0.6 and mean serial interval λ=6. (A) Time series generated by model, with cases as blue points and spillover hazard function given by green line. (B) Joint posterior distribution for R₀ and absolute spillover hazard from model inference when timing and relative amplitude of spillover hazard are known. True values are indicated by white dot. (C) Joint posterior distribution for R₀ and peak spillover hazard (i.e. middle step of hazard function) when amplitude and timings of the spillover hazard steps are unknown but the hazard drop date (e.g. date of market closure) is known. (D) Histogram of estimated value of R₀ from model inference using 200 different simulated time series, when neither amplitude nor timings of the spillover hazard steps are known. Each value is calculated as the median of the posterior distribution for R₀. Solid lines, R₀ in the simulated data. Dashed lines, the inferred value of R₀. (E) Histogram of estimated value of R₀ when relative amplitude and timings of the spillover hazard steps are known. (F) Histogram of estimated value of R₀ when amplitude and timings of the spillover hazard steps are unknown but the hazard drop date is known.

Simulation results when mean serial interval λ=3.

Results from inference using simulated time series with R₀ =0.6 and mean serial interval λ=3. (A) Time series generated by model. (B) Joint posterior distribution for R₀ and absolute spillover hazard from model inference when timing and relative amplitude of spillover hazard are known. (C) Joint posterior distribution for R₀ and peak spillover hazard when amplitude and timings of the spillover hazard steps are unknown but the hazard drop date is known. (D) Histogram of estimated value of R₀ from model inference using 200 different simulated time series, when neither amplitude nor timings of the spillover hazard steps are known. (E) Histogram of estimated value of R₀ when relative amplitude and timings of the spillover hazard steps are known. (F) Histogram of estimated value of R₀ when amplitude and timings of the spillover hazard steps are unknown but the hazard drop date is known.

Sensitivity to mis-specification of offspring distribution

Results from inference using simulated time series with R₀=0.6 and λ=6, with a negative binomial offspring distribution in simulations, and Poisson distribution in the inference model. (A) Histogram of estimated value of R0 from model inference using 200 different simulated time series, when neither amplitude nor timings of the spillover hazard steps are known. (B) Histogram of estimated value of R0 when relative amplitude and timings of the spillover hazard steps are known. (C) Histogram of estimated value of R0 when amplitude and timings of the spillover hazard steps are unknown but the hazard drop date is known.

Sensitivity to mis-specification of hazard function

Model inference when simulated spillover hazard depends on an exponential function, and inference model uses a step function. (A) Representative run when R0 =0.25 and λ=3. Blue points, simulated time series; green line, hazard function in the case generation model. (B) Histogram of median posterior distribution for R0 for 200 time series generated with λ=3. Black line shows true value of R0 =0.25; dashed line, median of inferred values. (C) Histogram of median posterior distribution for R0 for 200 such time series with λ=6.

Inference of proportion of human-human transmission

(A) Comparison of inferred proportion of cases resulting from human-human transmission and actual proportion, for 200 simulated timeseries, using a Poisson offspring distribution. (B) Comparison of inferred human-human cases and actual proportion when offspring distribution is negative binomial with shape parameter 0.1.

Estimates for R₀ and spillover hazard for A/H7N9 in China

Posterior estimates for spillover hazard (in this case resulting from live bird markets) and R₀ for influenza A/H7N9 in China, assuming a mean serial interval λ=9.6. (A) Case incidence for Shanghai and the spillover hazard from the best fitting model with market and human-to-human hazard: black dots, observed H7N9 cases; red shaded region, posterior distribution for amplitude of the spillover hazard. Inset: Posterior distribution for R₀ in Shanghai. (B) Case incidence for Jiangsu and inferred spillover hazard in best fitting model. (C) Case incidence for Zhejiang and inferred spillover hazard in best fitting model. (D) Estimated number of cases resulting from human-to-human transmission in different regions. Black points, total observed onsets; blue points, estimated non-index cases (with error bars representing 95% credible interval).

Sensitivity to under-reporting when drop in hazard known

Histograms of estimated value of R0 from model inference with simulated time series when only timing of drop in spillover hazard known. Market parameters are chosen so that a mean of 33 cases are observed, regardless of reporting rate. 200 different time series were simulated. Each value in the histogram is calculated as the median of the posterior distribution for R0. Solid lines, R₀ = 0.6 in the simulated data; dashed line, median of inferred values. Top row, serial interval is 3 days; middle row, 6 days; bottom row, 9.6 days. (A), (B) and (C) All cases observed. (D), (E) and (F) only 25% of cases observed. (G), (H) and (I) Only 1% of cases observed.

Sensitivity to under-reporting when shape of hazard known

Histograms of estimated value of R0 from model inference simulated time series when relative amplitude and timings of spillover hazard known. Market parameters are chosen so that a mean of 33 cases are observed, regardless of reporting rate. 200 different time series were simulated. Each value in the histogram is calculated as the median of the posterior distribution for R0. Solid lines, R0 = 0.6 in the simulated data. Top row, serial interval is 3 days; middle row, 6 days; bottom row, 9.6 days. (A), (B) and (C) All cases observed. (D), (E) and (F) only 25% of cases observed. (G), (H) and (I) Only 1% of cases observed.

Estimation of R₀ in real time

(A) Simulated time series, with cases as blue points and spillover hazard function given by green line. R₀ = 1.05 and λ = 6. (B) Real time estimate of R₀ when only the timing of drop in spillover hazard was known. Thick blue line, inferred estimate of R₀ at that point in time; blue shaded region, 95% credible interval; dashed line, true value of R₀. (C) Real time estimate of R₀ when shape of the spillover hazard but not the overall amplitude was known.