Fast protein folding kinetics
- PMID: 24641816
- PMCID: PMC4047647
- DOI: 10.1017/S003358351400002X
Fast protein folding kinetics
Abstract
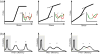
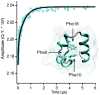
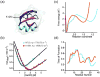
Fast-folding proteins have been a major focus of computational and experimental study because they are accessible to both techniques: they are small and fast enough to be reasonably simulated with current computational power, but have dynamics slow enough to be observed with specially developed experimental techniques. This coupled study of fast-folding proteins has provided insight into the mechanisms, which allow some proteins to find their native conformation well <1 ms and has uncovered examples of theoretically predicted phenomena such as downhill folding. The study of fast folders also informs our understanding of even 'slow' folding processes: fast folders are small; relatively simple protein domains and the principles that govern their folding also govern the folding of more complex systems. This review summarizes the major theoretical and experimental techniques used to study fast-folding proteins and provides an overview of the major findings of fast-folding research. Finally, we examine the themes that have emerged from studying fast folders and briefly summarize their application to protein folding in general, as well as some work that is left to do.
Figures

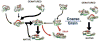

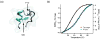
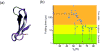
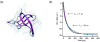




References
-
- Abbruzzetti S, Carcelli M, Pelagatti P, Rogolino D, Viappiani C. Photoinduced alkaline pH-jump on the nanosecond time scale. Chemical Physics Letters. 2001a;344:387–394.
-
- Abbruzzetti S, Viappiani C, Small JR, Libertini LJ, Small EW. Kinetics of histidine deligation from the heme in GuHCl-unfolded Fe(III) Cytochrome c studied by a laser-induced pH-jump technique. J Am Chem Soc. 2001b;123:6649–6653. - PubMed
-
- Ansari A, Jones CM, Henry ER, Hofrichter J, Eaton WA. The Role of Solvent Viscosity in th Dynamics of Protein Conformational Changes. Science. 1992;256:1797–1798. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

