Determining elasticity from single polymer dynamics

Abstract

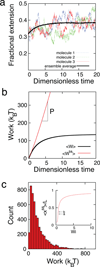
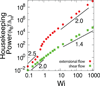
The ability to determine polymer elasticity and force-extension relations from polymer dynamics in flow has been challenging, mainly due to difficulties in relating equilibrium properties such as free energy to far-from-equilibrium processes. In this work, we determine polymer elasticity from the dynamic properties of polymer chains in fluid flow using recent advances in statistical mechanics. In this way, we obtain the force-extension relation for DNA from single molecule measurements of polymer dynamics in flow without the need for optical tweezers or bead tethers. We further employ simulations to demonstrate the practicality and applicability of this approach to the dynamics of complex fluids. We investigate the effects of flow type on this analysis method, and we develop scaling laws to relate the work relation to bulk polymer viscometric functions. Taken together, our results show that nonequilibrium work relations can play a key role in the analysis of soft material dynamics.

Fig. 1

Nonequilibrium work calculations for λ-DNA (contour length L ≈ 21 µm) in extensional flow. (a) Trajectories of fractional polymer extension induced by Wi = 0.63, wherein molecules are stretched from a fractional extension λ₁/L ≈ 0.32 (State a) to λ₂/L ≈ 0.38 (State b). Single molecule trajectories and the ensemble average stretch are shown. (b) Transient average work trajectories, where 〈W〉 is the average work for a process wherein polymer molecules are stretched from State a to State b, and 〈W^hk〉 is the housekeeping work required to maintain a polymer at an average steady state extension at State b. The slope of 〈W^hk〉 gives the housekeeping power P. (c) Histogram of work required to stretch single polymers from State a to State b. (Inset) Steady state fractional extension 〈x^ss〉/L as a function of Wi in extensional flow.

Fig. 2

(a) Free energy landscape for λ-DNA (L ≈ 21 µm) determined from nonequilibrium dynamics in extensional flow using the JE. (Inset) Free energy landscape for λ-DNA determined in tethered uniform flow using the JE. The free energy at zero extension is defined as the reference state (F_o = 0). (b) Polymer elasticity for λ-DNA (L ≈ 21 µm) determined from dynamic data in extensional flow using the JE. (Inset) Polymer elasticity for a polystyrene molecule (L ≈ 1.2 µm) determined in extensional flow using the JE. ILC: inverse Langevin chain force-extension relation.

Fig. 3

Application of the nonequilibrium work relation to experimental data on polymer dynamics. (a) Individual (light) and ensemble average (dark) stretching trajectories of 7-λ-DNA molecules in extensional flow at Wi = 0.75 obtained from prior single molecule polymer dynamics experiments. (Inset) Schematic of a stretched molecule in a planar extensional flow. (b) Free energy landscape determined from applying JE to experimental stretching trajectories. Solid line is the integrated Marko-Siggia (IMS) relation with contour length as fitting parameter. (Inset) Average dissipated work as a function of molecular extension. Data shown are mean values ± SD.

Fig. 4

Housekeeping power as a function of dimensionless flow strength Weissenberg number Wi in shear and extensional flow for λ-DNA using a dumbbell model, where λ_H = ζ/4H is the relaxation time of the corresponding Hookean polymer chain.