Early warning signals of ecological transitions: methods for spatial patterns

Abstract

A number of ecosystems can exhibit abrupt shifts between alternative stable states. Because of their important ecological and economic consequences, recent research has focused on devising early warning signals for anticipating such abrupt ecological transitions. In particular, theoretical studies show that changes in spatial characteristics of the system could provide early warnings of approaching transitions. However, the empirical validation of these indicators lag behind their theoretical developments. Here, we summarize a range of currently available spatial early warning signals, suggest potential null models to interpret their trends, and apply them to three simulated spatial data sets of systems undergoing an abrupt transition. In addition to providing a step-by-step methodology for applying these signals to spatial data sets, we propose a statistical toolbox that may be used to help detect approaching transitions in a wide range of spatial data. We hope that our methodology together with the computer codes will stimulate the application and testing of spatial early warning signals on real spatial data.

Figure 1. Spatial patterns along a degradation gradient in the three data sets.

In each row, the system approaches the bifurcation point from left to right (see Fig. S1 in Appendix S2 to visualize the location of the four snapshots along the degradation gradient.) First row: local positive feedback model (data set 1). Middle row: local facilitation model (data set 2). Bottom row: scale-dependent feedback model (data set 3). In each panel, darker cells correspond to higher vegetation biomass.

Figure 2. Flow chart of analysis to perform on a spatial data set.

Figure 3. Radial-spectrum along a degradation gradient in the three data sets.

In a row, each panel corresponds to the radial-spectrum of the system at a different location along the degradation gradient. The system approaches the bifurcation point from left to right column (as in Fig. 1). First row: local positive feedback model. Middle row: local facilitation model (original data transformed using 5×5 submatrices). Bottom row: scale-dependent feedback model. Gray areas correspond to 95% confidence intervals obtained using 200 simulations of a null model (i.e. data sets of same size generated by reshuffling the original data set).

Figure 4. Generic leading indicators in data sets 1 and 2 along a degradation gradient.

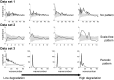
In each panel, the -values correspond to the rank of the snapshot of the system along the degradation gradient. This mimicks a scenario where we would not know the exact value of the driver but where we can order the data set along a degradation gradient and see Fig. S1 in Appendix S2 to visualize the location of the four snapshots along the degradation gradient. For each of the three data sets, 10 snapshots were used. Left: local positive feedback model (data set 1). Right: local facilitation model (data set 2; original data transformed using 5×5 sub-matrices). First row: spatial variance. Second row: spatial skewness. Third row: spatial correlation at lag one. In each panel, Kendall's , quantifying the trend of the indicator, is indicated. Gray areas correspond to 95% confidence intervals obtained using 200 simulations of a null model (i.e. data sets of same size generated by reshuffling the original data set).

Figure 5. Power spectrum along a degradation gradient in the three data sets.

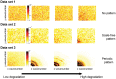
In a row, the system approaches the bifurcation point, from left to right column (as in Fig. 1). For a data set of size , the power spectrum is typically plotted for wavenumbers up to and and is scaled by the spatial variance (i.e. the scaled power spectrum is evaluated as ) . Red color indicates higher values of the scaled power spectrum, . The and -axis correspond to the wavenumbers along these directions. First row: local positive feedback model (data set 1). Middle row: local facilitation model (data set 2; original data transformed using 5×5 sub-matrices). Bottom row: scale-dependent feedback model (data set 3).

Figure 6. Inverse cumulative patch-size distributions along a degradation gradient in data sets 2 and 3.

Along each row, the system approaches the bifurcation point from left to right colum (as in Fig. 1)n. First row: local facilitation model (original data not transformed). Bottom row: scale-dependent feedback model. Gray areas corresponds to 95% confidence interval obtained using 200 simulations of a null model (i.e. data sets of same size generated by reshuffling the original matrix).

Figure 7. Analysis of the periodic patterns of data set 3.

In a row, the system approaches the bifurcation point from left to right column (as in Fig. 1). First row: -spectrum. Gray areas corresponds to 95% confidence interval obtained using 200 simulations of a null model (i.e. data sets of same size generated by reshuffling the original matrix). Second row: histogram of the values of the data set (or pixels of the image).

Figure 8. Generic leading indicators in data set 2 along a degradation gradient using different coarsening of the original data.

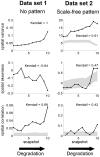
In each panel, the -value indicates the rank of the snapshot along the degradation gradient. This mimicks a scenario where we would not know the exact value of the driver but where we can order the data set along a gradient and See Fig. S1 in Appendix S2 to visualize the location of the four snapshots along the degradation gradient. Left: original data. Middle: original data transformed using 2×2 sub-matrices. Middle: original data transformed using 5×5 sub-matrices. First row: spatial variance. Second row: spatial skewness. Third row: spatial correlation at lag one. In each panel, Kendall's quantifies the strength of the trend of the indicator. Gray areas correspond to 95% confidence intervals obtained using 200 simulations of a null model (i.e. data sets of same size generated by reshuffling the original matrix).