Complex role of space in the crossing of fitness valleys by asexual populations
- PMID: 24671934
- PMCID: PMC4006240
- DOI: 10.1098/rsif.2014.0014
Complex role of space in the crossing of fitness valleys by asexual populations
Abstract
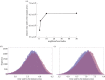
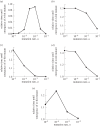
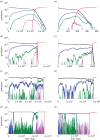
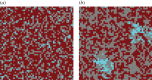
The evolution of complex traits requires the accumulation of multiple mutations, which can be disadvantageous, neutral or advantageous relative to the wild-type. We study two spatial (two-dimensional) models of fitness valley crossing (the constant-population Moran process and the non-constant-population contact process), varying the number of loci involved and the degree of mixing. We find that spatial interactions accelerate the crossing of fitness valleys in the Moran process in the context of neutral and disadvantageous intermediate mutants because of the formation of mutant islands that increase the lifespan of mutant lineages. By contrast, in the contact process, spatial structure can accelerate or delay the emergence of the complex trait, and there can even be an optimal degree of mixing that maximizes the rate of evolution. For advantageous intermediate mutants, spatial interactions always delay the evolution of complex traits, in both the Moran and contact processes. The role of the mutant islands here is the opposite: instead of protecting, they constrict the growth of mutants. We conclude that the laws of population growth can be crucial for the effect of spatial interactions on the rate of evolution, and we relate the two processes explored here to different biological situations.
Keywords: complex phenotype; mutations; sequential evolution; stochastic tunnelling.
Figures


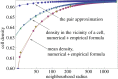

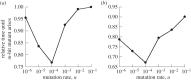
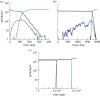
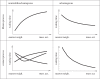
References
-
- Whitlock MC, Phillips PC, Moore FBG, Tonsor SJ. 1995. Multiple fitness peaks and epistasis. Annu. Rev. Ecol. Syst. 26, 601–629. ( 10.1146/annurev.es.26.110195.003125) - DOI
-
- Weinreich DM, Chao L. 2005. Rapid evolutionary escape by large populations from local fitness peaks is likely in nature. Evolution 59, 1175–1182. - PubMed
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
