SWIFT-scalable clustering for automated identification of rare cell populations in large, high-dimensional flow cytometry datasets, part 1: algorithm design

Abstract

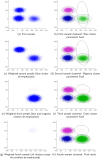
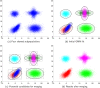
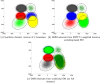
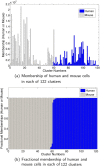
We present a model-based clustering method, SWIFT (Scalable Weighted Iterative Flow-clustering Technique), for digesting high-dimensional large-sized datasets obtained via modern flow cytometry into more compact representations that are well-suited for further automated or manual analysis. Key attributes of the method include the following: (a) the analysis is conducted in the multidimensional space retaining the semantics of the data, (b) an iterative weighted sampling procedure is utilized to maintain modest computational complexity and to retain discrimination of extremely small subpopulations (hundreds of cells from datasets containing tens of millions), and (c) a splitting and merging procedure is incorporated in the algorithm to preserve distinguishability between biologically distinct populations, while still providing a significant compaction relative to the original data. This article presents a detailed algorithmic description of SWIFT, outlining the application-driven motivations for the different design choices, a discussion of computational complexity of the different steps, and results obtained with SWIFT for synthetic data and relatively simple experimental data that allow validation of the desirable attributes. A companion paper (Part 2) highlights the use of SWIFT, in combination with additional computational tools, for more challenging biological problems.

Keywords: Gaussian mixture models; automated multivariate clustering; ground truth data; rare subpopulation detection; weighted sampling.

Figure 1

The SWIFT algorithm: (a) Overall workflow and (b) Weighted iterative sampling.

Figure 2

Weighted iterative sampling based Gaussian mixture model (GMM) clustering for better estimation of smaller subpopulations. Intermediate results along different stages of the algorithm and the final result are shown highlighting how smaller subpopulations are emphasized in the weighted iterative sampling process. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 3

Cluster merging in SWIFT illustrated via a 2D example: (a) Four original skewed subpopulations, (b) Initial GMM fit, (c) Potential pairs considered for merging, the bounding box filtering introduced for computational efficiency eliminates all pairs except , and ,, and (d) Resulting clusters after merging. Note that in the final result, the original skewed and non-Gaussian subpopulations are well-represented via the merged clusters formed from combining initially fit Gaussians. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 4

Comparison of weighted sampling based EM and the traditional EM algorithm on a synthetic mixture of 6 Gaussians: (a) Original dataset, (b) GMM estimate from the weighted sampling based EM used in SWIFT, and (c) GMM estimate from traditional EM algorithm. Note that smallest subpopulation is missed by the traditional EM algorithm but is represented with good accuracy by the weighted sampling based EM used in SWIFT. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 5

Results from SWIFT clustering of the known-ground-truth, electronically mixed, human-mouse dataset. SWIFT yields 122 clusters that clearly separate the human vs. mouse cells: most clusters are comprised of entirely human or entirely mouse cells. See text and caption for Supporting Information Fig. S.12 for details of the dataset. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]