Reduced model captures Mg(2+)-RNA interaction free energy of riboswitches
- PMID: 24703312
- PMCID: PMC3976530
- DOI: 10.1016/j.bpj.2014.01.042
Reduced model captures Mg(2+)-RNA interaction free energy of riboswitches
Abstract
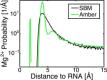
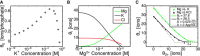
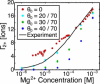
The stability of RNA tertiary structures depends heavily on Mg(2+). The Mg(2+)-RNA interaction free energy that stabilizes an RNA structure can be computed experimentally through fluorescence-based assays that measure Γ2+, the number of excess Mg(2+) associated with an RNA molecule. Previous explicit-solvent simulations predict that the majority of excess Mg(2+) ions interact closely and strongly with the RNA, unlike monovalent ions such as K(+), suggesting that an explicit treatment of Mg(2+) is important for capturing RNA dynamics. Here we present a reduced model that accurately reproduces the thermodynamics of Mg(2+)-RNA interactions. This model is able to characterize long-timescale RNA dynamics coupled to Mg(2+) through the explicit representation of Mg(2+) ions. KCl is described by Debye-Hückel screening and a Manning condensation parameter, which represents condensed K(+) and models its competition with condensed Mg(2+). The model contains one fitted parameter, the number of condensed K(+) ions in the absence of Mg(2+). Values of Γ2+ computed from molecular dynamics simulations using the model show excellent agreement with both experimental data on the adenine riboswitch and previous explicit-solvent simulations of the SAM-I riboswitch. This agreement confirms the thermodynamic accuracy of the model via the direct relation of Γ2+ to the Mg(2+)-RNA interaction free energy, and provides further support for the predictions from explicit-solvent calculations. This reduced model will be useful for future studies of the interplay between Mg(2+) and RNA dynamics.
Copyright © 2014 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures
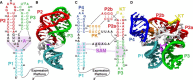

Similar articles
-
A magnesium-induced triplex pre-organizes the SAM-II riboswitch.PLoS Comput Biol. 2017 Mar 1;13(3):e1005406. doi: 10.1371/journal.pcbi.1005406. eCollection 2017 Mar. PLoS Comput Biol. 2017. PMID: 28248966 Free PMC article.
-
Using simulations and kinetic network models to reveal the dynamics and functions of riboswitches.Methods Enzymol. 2015;553:235-58. doi: 10.1016/bs.mie.2014.10.062. Epub 2015 Feb 3. Methods Enzymol. 2015. PMID: 25726468 Free PMC article.
-
Cooperation between Magnesium and Metabolite Controls Collapse of the SAM-I Riboswitch.Biophys J. 2017 Jul 25;113(2):348-359. doi: 10.1016/j.bpj.2017.06.044. Biophys J. 2017. PMID: 28746845 Free PMC article.
-
[The adenine riboswitch: a new gene regulation mechanism].Med Sci (Paris). 2006 Dec;22(12):1053-9. doi: 10.1051/medsci/200622121053. Med Sci (Paris). 2006. PMID: 17156726 Review. French.
-
Computational prediction of riboswitches.Methods Enzymol. 2015;553:287-312. doi: 10.1016/bs.mie.2014.10.063. Epub 2015 Feb 19. Methods Enzymol. 2015. PMID: 25726470 Review.
Cited by
-
Directional translocation resistance of Zika xrRNA.Nat Commun. 2020 Jul 27;11(1):3749. doi: 10.1038/s41467-020-17508-7. Nat Commun. 2020. PMID: 32719310 Free PMC article.
-
A New Method to Predict Ion Effects in RNA Folding.Methods Mol Biol. 2017;1632:1-17. doi: 10.1007/978-1-4939-7138-1_1. Methods Mol Biol. 2017. PMID: 28730429 Free PMC article.
-
Ligand Modulates Cross-Coupling between Riboswitch Folding and Transcriptional Pausing.Mol Cell. 2018 Nov 1;72(3):541-552.e6. doi: 10.1016/j.molcel.2018.08.046. Mol Cell. 2018. PMID: 30388413 Free PMC article.
-
Implicit Solvent with Explicit Ions Generalized Born Model in Molecular Dynamics: Application to DNA.J Chem Theory Comput. 2024 Oct 8;20(19):8724-8739. doi: 10.1021/acs.jctc.4c00833. Epub 2024 Sep 16. J Chem Theory Comput. 2024. PMID: 39283928 Free PMC article.
-
Exploring the Energy Landscape of Riboswitches Using Collective Variables Based on Tertiary Contacts.J Mol Biol. 2022 Sep 30;434(18):167788. doi: 10.1016/j.jmb.2022.167788. Epub 2022 Aug 11. J Mol Biol. 2022. PMID: 35963460 Free PMC article.
References
-
- Onuchic J.N., Luthey-Schulten Z., Wolynes P.G. Theory of protein folding: the energy landscape perspective. Annu. Rev. Phys. Chem. 1997;48:545–600. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

