Revealing mesoscopic structural universality with diffusion
- PMID: 24706873
- PMCID: PMC3986157
- DOI: 10.1073/pnas.1316944111
Revealing mesoscopic structural universality with diffusion
Abstract
Measuring molecular diffusion is widely used for characterizing materials and living organisms noninvasively. This characterization relies on relations between macroscopic diffusion metrics and structure at the mesoscopic scale commensurate with the diffusion length. Establishing such relations remains a fundamental challenge, hindering progress in materials science, porous media, and biomedical imaging. Here we show that the dynamical exponent in the time dependence of the diffusion coefficient distinguishes between the universality classes of the mesoscopic structural complexity. Our approach enables the interpretation of diffusion measurements by objectively selecting and modeling the most relevant structural features. As an example, the specific values of the dynamical exponent allow us to identify the relevant mesoscopic structure affecting MRI-measured water diffusion in muscles and in brain, and to elucidate the structural changes behind the decrease of diffusion coefficient in ischemic stroke.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
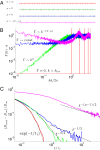
 (see Examples of Structural Universality Classes). (C) Numerical results confirming the relation 1. The time-dependence 3 clearly distinguishes between the four arrangements, while the value
(see Examples of Structural Universality Classes). (C) Numerical results confirming the relation 1. The time-dependence 3 clearly distinguishes between the four arrangements, while the value  is the same for all of them. The dashed lines are the exact power laws from
is the same for all of them. The dashed lines are the exact power laws from  ; here
; here  .
.
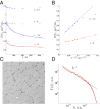
 in
in  , provided by the muscle fiber membrane (sarcolemma). (A) The longitudinal,
, provided by the muscle fiber membrane (sarcolemma). (A) The longitudinal,  , and the transverse,
, and the transverse,  , diffusion tensor components for calf tongue genioglossus (TG) (blue circles) and heart (H) (red diamonds). Solid lines are the fit of
, diffusion tensor components for calf tongue genioglossus (TG) (blue circles) and heart (H) (red diamonds). Solid lines are the fit of  to
to  derived from
derived from  . For fit results see
. For fit results see  replotted as function of
replotted as function of  consistent with
consistent with  . Eq. 1 yields
. Eq. 1 yields  ; hence,
; hence,  (see Extended Disorder Provided by Muscle Fiber Walls and Fig. 2C). (C) Muscle slice across the fibers. (D)
(see Extended Disorder Provided by Muscle Fiber Walls and Fig. 2C). (C) Muscle slice across the fibers. (D)  calculated from image intensity in C. Tight cell packing achieved by straight cell walls in C results in exponent
calculated from image intensity in C. Tight cell packing achieved by straight cell walls in C results in exponent  of the extended disorder class of Fig. 2C, yielding
of the extended disorder class of Fig. 2C, yielding  .
.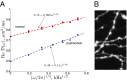
 in cerebral gray matter consistent with
in cerebral gray matter consistent with  diffusion along narrow neurites in the presence of short-range disorder
diffusion along narrow neurites in the presence of short-range disorder  , both in normal and globally ischemic rat brain. (A) Original data (20) for d-sin and cos gradient waveforms, fitted to Eq. 6, yields
, both in normal and globally ischemic rat brain. (A) Original data (20) for d-sin and cos gradient waveforms, fitted to Eq. 6, yields  for normal and
for normal and  for postmortem brain. The role of the disorder (the slope) increases after global ischemia onset. (B) Varicose axons from rat hippocampus area CA1 (22) rationalizing the picture of an effectively 1D diffusion inside narrow randomly oriented and structurally disordered neurites.
for postmortem brain. The role of the disorder (the slope) increases after global ischemia onset. (B) Varicose axons from rat hippocampus area CA1 (22) rationalizing the picture of an effectively 1D diffusion inside narrow randomly oriented and structurally disordered neurites.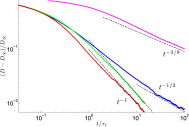
 . For
. For  and
and  (blue represents short-range disorder and magenta strong disorder), the power law in
(blue represents short-range disorder and magenta strong disorder), the power law in  coincides with that in
coincides with that in  (in accord with Eq. 5) whereas for
(in accord with Eq. 5) whereas for  (red represents periodic and green hyperuniform), it is masked by the
(red represents periodic and green hyperuniform), it is masked by the  term. Taking the derivative
term. Taking the derivative  reveals the values of ϑ (as shown in Fig. 1) but increases noise.
reveals the values of ϑ (as shown in Fig. 1) but increases noise.References
-
- Haus JW, Kehr KW. Diffusion in regular and disordered lattices. Phys Rep. 1987;150(5-6):263–406.
-
- Bouchaud JP, Georges A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys Rep. 1990;195(4-5):127–293.
-
- Kusumi A, et al. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: High-speed single-molecule tracking of membrane molecules. Annu Rev Biophys Biomol Struct. 2005;34:351–378. - PubMed
-
- Callaghan PT. Principles of Nuclear Magnetic Resonance Microscopy. Oxford: Clarendon; 1991.
-
- Mitra PP, Sen PN, Schwartz LM, Le Doussal P. Diffusion propagator as a probe of the structure of porous media. Phys Rev Lett. 1992;68(24):3555–3558. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

