Bending forces plastically deform growing bacterial cell walls
- PMID: 24711421
- PMCID: PMC4000856
- DOI: 10.1073/pnas.1317497111
Bending forces plastically deform growing bacterial cell walls
Abstract
Cell walls define a cell's shape in bacteria. The walls are rigid to resist large internal pressures, but remarkably plastic to adapt to a wide range of external forces and geometric constraints. Currently, it is unknown how bacteria maintain their shape. In this paper, we develop experimental and theoretical approaches and show that mechanical stresses regulate bacterial cell wall growth. By applying a precisely controllable hydrodynamic force to growing rod-shaped Escherichia coli and Bacillus subtilis cells, we demonstrate that the cells can exhibit two fundamentally different modes of deformation. The cells behave like elastic rods when subjected to transient forces, but deform plastically when significant cell wall synthesis occurs while the force is applied. The deformed cells always recover their shape. The experimental results are in quantitative agreement with the predictions of the theory of dislocation-mediated growth. In particular, we find that a single dimensionless parameter, which depends on a combination of independently measured physical properties of the cell, can describe the cell's responses under various experimental conditions. These findings provide insight into how living cells robustly maintain their shape under varying physical environments.
Keywords: cell shape; defects; dislocation; elasticity; peptidoglycan.
Conflict of interest statement
The authors declare no conflict of interest.
Figures


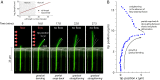
 17 min, in the absence of the flow, the cell straightens gradually as it grows. (A, Upper) The length of the cell increases exponentially despite the large deflections induced by the external mechanical forces—the mass-doubling time does not change appreciably during the experiment and is comparable to that of nonfilamentous cells. (B) Scatter plot of the experimental results for the tip position as time progresses through the snap-back experiment from A.
17 min, in the absence of the flow, the cell straightens gradually as it grows. (A, Upper) The length of the cell increases exponentially despite the large deflections induced by the external mechanical forces—the mass-doubling time does not change appreciably during the experiment and is comparable to that of nonfilamentous cells. (B) Scatter plot of the experimental results for the tip position as time progresses through the snap-back experiment from A.

References
-
- Janmey PA, Weitz DA. Dealing with mechanics: Mechanisms of force transduction in cells. Trends Biochem Sci. 2004;29(7):364–370. - PubMed
-
- Discher DE, Janmey P, Wang YL. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310(5751):1139–1143. - PubMed
-
- Aharoni H, Abraham Y, Elbaum R, Sharon E, Kupferman R. Emergence of spontaneous twist and curvature in non-euclidean rods: Application to Erodium plant cells. Phys Rev Lett. 2012;108(23):238106. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

