Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2014 Apr 8:4:4603.
doi: 10.1038/srep04603.

Generalized friendship paradox in complex networks: the case of scientific collaboration

Young-Ho Eom  1 , Hang-Hyun Jo  2
Affiliations

Generalized friendship paradox in complex networks: the case of scientific collaboration

Young-Ho Eom et al. Sci Rep. .

Abstract

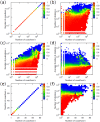
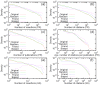
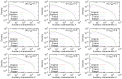
The friendship paradox states that your friends have on average more friends than you have. Does the paradox "hold" for other individual characteristics like income or happiness? To address this question, we generalize the friendship paradox for arbitrary node characteristics in complex networks. By analyzing two coauthorship networks of Physical Review journals and Google Scholar profiles, we find that the generalized friendship paradox (GFP) holds at the individual and network levels for various characteristics, including the number of coauthors, the number of citations, and the number of publications. The origin of the GFP is shown to be rooted in positive correlations between degree and characteristics. As a fruitful application of the GFP, we suggest effective and efficient sampling methods for identifying high characteristic nodes in large-scale networks. Our study on the GFP can shed lights on understanding the interplay between network structure and node characteristics in complex networks.

PubMed Disclaimer

Figures

Figure 1
Figure 1. The paradox holding probability h(k, x) as a function of degree k and node characteristic x.
For the Physical Review (PR) coauthorship network, we use (a) the number of coauthors, i.e., x = k, (b) the number of citations, (c) the number of publication, and (d) the average number of citations per publication, while for the Google Scholar (GS) coauthorship network, we use (e) the number of coauthors, i.e., x = k, and (f) the number of citations.
Figure 2
Figure 2. Characteristic distributions for control group, friend group, and biased group, for each of which 5000 nodes are sampled.
The original full distributions are also plotted for comparison. We use (a) the number of coauthors (PR), (b) the number of citations (PR), (c) the number of publications (PR), (d) the average number of citations per publication (PR), (e) the number of coauthors (GS), and (f) the number of citations (GS).
Figure 3
Figure 3. Performance comparison of control group, friend group, and biased group for auxiliary characteristics X with various values of correlation with degree: .
For each value of ρkX, 1000 random configurations are generated, for each of which 5000 nodes are sampled as in Fig. 2.
See this image and copyright information in PMC

References

    1. Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). - PubMed
    1. Castello C., Fortunato S. & Loreto V. Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646 (2009).
    1. Lazer D. et al. Computational social science. Science 323, 721–723 (2009). - PMC - PubMed
    1. Vespignani A. Modelling dynamical processes in complex socio-technical systems. Nat. Phy. 8, 32–39 (2011).
    1. Centola D. The spread of behavior in an online social network experiment. Science 329, 1194–1197 (2010). - PubMed

Publication types