Cosinor-based rhythmometry

Abstract

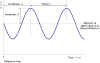
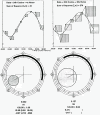
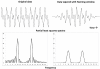
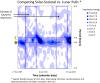
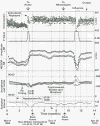
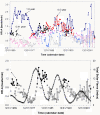
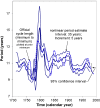
A brief overview is provided of cosinor-based techniques for the analysis of time series in chronobiology. Conceived as a regression problem, the method is applicable to non-equidistant data, a major advantage. Another dividend is the feasibility of deriving confidence intervals for parameters of rhythmic components of known periods, readily drawn from the least squares procedure, stressing the importance of prior (external) information. Originally developed for the analysis of short and sparse data series, the extended cosinor has been further developed for the analysis of long time series, focusing both on rhythm detection and parameter estimation. Attention is given to the assumptions underlying the use of the cosinor and ways to determine whether they are satisfied. In particular, ways of dealing with non-stationary data are presented. Examples illustrate the use of the different cosinor-based methods, extending their application from the study of circadian rhythms to the mapping of broad time structures (chronomes).

Figure 1

Definition of rhythm characteristics. The MESOR is a rhythm-adjusted mean; the double amplitude (2A) is a measure of the extent of predictable change within a cycle; the acrophase is a measure of the timing of overall high values recurring in each cycle, expressed in (negative) degrees in relation to a reference time set to 0°, with 360° equated to the period; and the period is the duration of one cycle. © Halberg Chronobiology Center.

Figure 2

Single-component single cosinor: hypothesis testing and parameter estimation. A cosine curve with a given period is fitted to the data (top) by least squares. This approach consists of minimizing the sum of squared deviations between the data and the fitted cosine curve. The larger this residual sum of squares is, the greater the uncertainty of the estimated parameters is. This is illustrated by the elliptical 95% confidence region for the amplitude-acrophase pair (bottom). When the error ellipse does not cover the pole, the zero-amplitude (no-rhythm) test is rejected and the alternative hypothesis holds that a rhythm with the given period is present in the data (left). Conservative 95% confidence limits for the amplitude and acrophase can then be obtained by drawing concentric circles and radii tangent to the error ellipse, respectively. When the error ellipse covers the pole, the null hypothesis of no-rhythm (zero amplitude) is accepted (right). Results (P-value from the zero-amplitude test, percentage rhythm or proportion of the overall variance accounted for by the fitted model, MESOR ± SE, amplitude and 95% confidence limits, acrophase and 95% confidence limits) are listed in each case. © Halberg Chronobiology Center.

Figure 3

Multiple-component single cosinor. Systolic blood pressure data collected over 7 days by a 45-year old woman fitted with a 24-hour cosine curve indicate the presence of lack of fit, departure from normality of residuals, and inhomogeneity of variance (left). The addition of a 12-hour component (middle) to the model (right) yields a better fit for which underlying assumptions are validated. © Halberg Chronobiology Center.

Figure 4

Elliptical confidence limits. The outer ellipse delineates the 95% confidence region for the joint estimation of the amplitude and acrophase (as a pair). Distances and tangents drawn from the pole to this outer ellipse yield conservative 95% confidence limits for the amplitude and acrophase considered separately as the area thus delineated is larger than the area of the outer ellipse. In order to obtain separate 95% confidence limits for the amplitude and acrophase, distances and tangents need to be drawn to a somewhat smaller (inner) ellipse. For further details, see [43]. © Halberg Chronobiology Center.

Figure 5

Effect of applying a Hanning taper on the least squares spectrum. A simulated signal consisting of a fundamental and second harmonic of equal amplitudes sampled over 10 cycles (top left) is tapered with a Hanning window (top right). Corresponding least squares spectra (bottom) indicate that while the spectral location of the two peaks remains the same, the amplitudes are reduced and the bandwidths are wider. Sidelobes are also greatly diminished. Simulation and original drawings from C. Lee-Gierke. © Halberg Chronobiology Center.

Figure 6

Gliding spectral window (surface chart). Systolic blood pressure was automatically measured around the clock by a 62-year old woman with recurring episodes of adynamic depression occurring twice a year and lasting 2–3 months. Complementary nonlinear analyses (not shown) indicate the coexistence of about 24.0- and 24.8-hour components, their relative prominence alternating between wellness and adynamic depression. Changes in the most prominent circadian period as a function of time are apparent from the changes in amplitude (shading) and location along the vertical scale. © Halberg Chronobiology Center.

Figure 7

Chronobiologic serial section. Peak expiratory flow was self-measured several times a day by a 53-year old man. The data covering a 14-month span are shown in row 1. They are analyzed in a 20-day interval progressively displaced by 2 days. Data in each interval are fitted with a 24-hour cosine curve. From the P-values shown in row 2, it can be seen that the circadian rhythm was detected with statistical significance most of the time, except for two short spans, one coinciding with a transmeridian flight (when fewer data were collected, row 5) and the other with influenza. Whereas the 24-hour acrophase remains relatively stable throughout the record (row 4), the MESOR (row 3, lower curve) and to a lesser extent the circadian amplitude (row 3, distance between the two curves) undergo sharp changes, notably in association with the influenza and earlier with a change in treatment timing. © Halberg Chronobiology Center.

Figure 8

Multiple-component serial section. Heart rate, self-measured a few times each day by a healthy man over several decades, was averaged over consecutive weeks. The weekly averages are fitted with a 3-component model consisting of cosine curves with periods of 1.0, 0.5, and 0.41 year in a 4-year interval moved by 0.2 year throughout the entire record. The time course of amplitudes of the 3 components is shown on top. Solid-filled, light-filled and empty symbols correspond to P-values <0.05, 0.05 < P < 0.10, and >0.10 from the zero-amplitude tests, respectively. Results for the 0.41-year component are reproduced below, where they are compared with the solar flare index that had been reported by physicists to be characterized by an about 5-month (0.41-year) component. 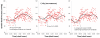The prominence of the about 5-month component in human heart rate follows an about 11-year cycle, which is similar to that characterizing solar flares. © Halberg Chronobiology Center.

Figure 9

Nonlinear serial section. The period of the about 11-year cycle in solar activity is estimated by nonlinear least squares applied to yearly Wolf numbers analyzed in a 35-year interval progressively moved by 5 years throughout the time series. The solar activity cycle has a period that can vary from about 9 to 15 years, shown here with its 95% confidence interval and compared with the official cycle length. © Halberg Chronobiology Center.