Comparative performance of four single extreme outlier discordancy tests from Monte Carlo simulations
- PMID: 24737992
- PMCID: PMC3967640
- DOI: 10.1155/2014/746451
Comparative performance of four single extreme outlier discordancy tests from Monte Carlo simulations
Abstract
Using highly precise and accurate Monte Carlo simulations of 20,000,000 replications and 102 independent simulation experiments with extremely low simulation errors and total uncertainties, we evaluated the performance of four single outlier discordancy tests (Grubbs test N2, Dixon test N8, skewness test N14, and kurtosis test N15) for normal samples of sizes 5 to 20. Statistical contaminations of a single observation resulting from parameters called δ from ±0.1 up to ±20 for modeling the slippage of central tendency or ε from ±1.1 up to ±200 for slippage of dispersion, as well as no contamination (δ = 0 and ε = ±1), were simulated. Because of the use of precise and accurate random and normally distributed simulated data, very large replications, and a large number of independent experiments, this paper presents a novel approach for precise and accurate estimations of power functions of four popular discordancy tests and, therefore, should not be considered as a simple simulation exercise unrelated to probability and statistics. From both criteria of the Power of Test proposed by Hayes and Kinsella and the Test Performance Criterion of Barnett and Lewis, Dixon test N8 performs less well than the other three tests. The overall performance of these four tests could be summarized as N2≅N15 > N14 > N8.
Figures
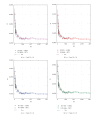
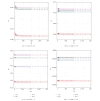
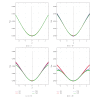
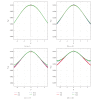
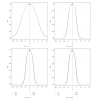
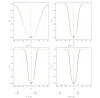
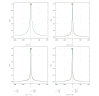
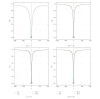
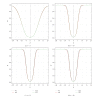
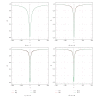
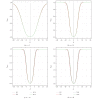
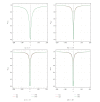
Similar articles
-
A Monte Carlo evaluation of growth mixture modeling.Dev Psychopathol. 2022 Oct;34(4):1604-1617. doi: 10.1017/S0954579420002230. Epub 2021 Mar 15. Dev Psychopathol. 2022. PMID: 33719983
-
Parametric and nonparametric population methods: their comparative performance in analysing a clinical dataset and two Monte Carlo simulation studies.Clin Pharmacokinet. 2006;45(4):365-83. doi: 10.2165/00003088-200645040-00003. Clin Pharmacokinet. 2006. PMID: 16584284
-
An enhanced Monte Carlo outlier detection method.J Comput Chem. 2015 Sep 30;36(25):1902-6. doi: 10.1002/jcc.24026. Epub 2015 Jul 31. J Comput Chem. 2015. PMID: 26226927
-
Removing the effect of statistical uncertainty on dose-volume histograms from Monte Carlo dose calculations.Phys Med Biol. 2000 Aug;45(8):2151-61. doi: 10.1088/0031-9155/45/8/307. Phys Med Biol. 2000. PMID: 10958186
-
A review of tests for exponentiality with Monte Carlo comparisons.J Appl Stat. 2020 Dec 4;49(5):1277-1304. doi: 10.1080/02664763.2020.1854202. eCollection 2022. J Appl Stat. 2020. PMID: 35707514 Free PMC article. Review.
Cited by
-
Traffic speed data imputation method based on tensor completion.Comput Intell Neurosci. 2015;2015:364089. doi: 10.1155/2015/364089. Epub 2015 Mar 3. Comput Intell Neurosci. 2015. PMID: 25866501 Free PMC article.
-
Immunization with a heat-killed preparation of the environmental bacterium Mycobacterium vaccae promotes stress resilience in mice.Proc Natl Acad Sci U S A. 2016 May 31;113(22):E3130-9. doi: 10.1073/pnas.1600324113. Epub 2016 May 16. Proc Natl Acad Sci U S A. 2016. PMID: 27185913 Free PMC article.
-
Outlier detection method in linear regression based on sum of arithmetic progression.ScientificWorldJournal. 2014;2014:821623. doi: 10.1155/2014/821623. Epub 2014 Jul 10. ScientificWorldJournal. 2014. PMID: 25121139 Free PMC article.
-
Commentary: Arnica Montana Effects on Gene Expression in a Human Macrophage Cell Line: Evaluation by Quantitative Real-Time PCR.Front Immunol. 2016 Sep 8;7:280. doi: 10.3389/fimmu.2016.00280. eCollection 2016. Front Immunol. 2016. PMID: 27660630 Free PMC article. No abstract available.
-
Identifying Patterns of Clinical Interest in Clinicians' Treatment Preferences: Hypothesis-free Data Science Approach to Prioritizing Prescribing Outliers for Clinical Review.JMIR Med Inform. 2022 Dec 20;10(12):e41200. doi: 10.2196/41200. JMIR Med Inform. 2022. PMID: 36538350 Free PMC article.
References
-
- Barnett V, Lewis T. Outliers in Statistical Data. 3rd edition. Chichester, UK: John Wiley & Sons; 1994.
-
- Dixon WJ. Analysis of extreme values. Annals of Mathematical Statistics. 1950;21(4):488–506.
-
- Ferguson TS. Rules for rejection of outliers. Revue de l'Institut International de Statistique. 1961;29(3):29–43.
-
- Shapiro SS, Wilk MB, Chen HJ. A comparative study of various tests for normality. Journal of American Statistical Association. 1968;63(324):1343–1371.
-
- Hawkins DM. Analysis of three tests for one or two outliers. Statistica Nederlandica. 1978;32(3):137–148.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources

