Can we identify non-stationary dynamics of trial-to-trial variability?

Abstract

Identifying sources of the apparent variability in non-stationary scenarios is a fundamental problem in many biological data analysis settings. For instance, neurophysiological responses to the same task often vary from each repetition of the same experiment (trial) to the next. The origin and functional role of this observed variability is one of the fundamental questions in neuroscience. The nature of such trial-to-trial dynamics however remains largely elusive to current data analysis approaches. A range of strategies have been proposed in modalities such as electro-encephalography but gaining a fundamental insight into latent sources of trial-to-trial variability in neural recordings is still a major challenge. In this paper, we present a proof-of-concept study to the analysis of trial-to-trial variability dynamics founded on non-autonomous dynamical systems. At this initial stage, we evaluate the capacity of a simple statistic based on the behaviour of trajectories in classification settings, the trajectory coherence, in order to identify trial-to-trial dynamics. First, we derive the conditions leading to observable changes in datasets generated by a compact dynamical system (the Duffing equation). This canonical system plays the role of a ubiquitous model of non-stationary supervised classification problems. Second, we estimate the coherence of class-trajectories in empirically reconstructed space of system states. We show how this analysis can discern variations attributable to non-autonomous deterministic processes from stochastic fluctuations. The analyses are benchmarked using simulated and two different real datasets which have been shown to exhibit attractor dynamics. As an illustrative example, we focused on the analysis of the rat's frontal cortex ensemble dynamics during a decision-making task. Results suggest that, in line with recent hypotheses, rather than internal noise, it is the deterministic trend which most likely underlies the observed trial-to-trial variability. Thus, the empirical tool developed within this study potentially allows us to infer the source of variability in in-vivo neural recordings.

Figure 1. Duffing non-linear oscillator (Equation 1, see parameter values in Methods).

(A) A small perturbation leading to a subtle drift in the relative distance between fixed points. Each subplot shows trajectories (i.e. different initial conditions randomly drawn, see text). Light red (left) and blue (right) lines indicate an example of a trajectory that changes its class (i.e. it is attracted to the opposite sink) after the small perturbation induced. Insets show class-posterior probabilities of each phase space vector belonging to the basin of attraction of one of the two sinks (see Methods for details). Two stars (**) indicate significant differences between means in the x-axis at ; which remain after a subtle variation in the of the perturbation parameter of the Duffing system. (B) and (C): Perturbation in other parameters induces bifurcations leading to chaotic oscillations (B) or global limit cycles (C) e.g. . As in plot A, inset shows the class-posteriors, which are severely transformed after such parameter variations.

Figure 2. Trajectory behaviour in Duffing systems.

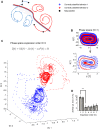
(A) Schema illustrating convergent trajectories with respect to attracting state boundaries (see also Figure S1). (B) Phase space flow (using initial conditions). (C) Projection into the three maximally discriminating directions (gram-schmidt ortonomalized) of an expanded space of order three. (D) This optimally regularized discriminant was used to compute the 20-fold cross validation of the trajectory incoherence index (TI) i.e. those different from any of the trajectories shown in plot (A) across initial conditions. The expansion order 3 yields to a maximal out-of-sample convergence; highly significant with respect to the phase space () shown in plot B (, see main text).

Figure 3. Non-autonomous drift in a non-linear dynamical system (unforced Duffing oscillator).

(c.f. Figure S1). (A) Example of a linear variation in the perturbation term (see also Equation 1). As fixed points approach each other, few trajectories change the basin of attraction and thus the class-membership. (B) Optimally regularized kernel-fisher discriminant in a third order expanded space was used to compute the classification error (CE) and trajectory incoherence (TI) as the distance between fixed point varies (shown mean values of 1000 initial conditions for each trial, error bars are SEM). The discriminant subspace is computed for the first trial and then fixed and applied to subsequent trials (note that only validation results from trials 2–14 are shown in the figure). Insets show amplified versions. Both CE (bottom inset) and TI (top inset) increase over trials, but TI enables us to detect, on a single trial basis, when a significant change occurs. When the temporal contingency within each trajectory is disrupted (bootstrap data, middle inset) TI is no longer sensitive to trial-to-trial variations, indicating the absence of a deterministic trend driving the observed dynamics. When bootstraps are generated by randomly sampling the increment of (from a uniform distribution of the same range), no trend in TI is observed either (thin grey line), as expected. These results are fully in line with statistical analyses shown in Figures S1B and S1C.

Figure 4. In vivo neural ensemble recordings in rat frontal cortex.

(A) Example of a delay-coordinate map expanded to a third order state space; see Methods and [48]) projected onto the three maximally discriminating dimensions (ortonormalized). Different colours correspond to different stages of the task (a radial arm-maze, inset left). (B) A clockwise rotation of the task-stage states from trial to trial seems to take place, suggesting a deterministic drift in the putatively attracting sets associated with task epochs. (C) Non-stationary drift in ensemble recordings. Analyses on an expanded space of third order where optimised for the first trial, the maximally discriminant subspace is fixed and then used to compute CE and TI in the next trials. As in the theoretical model (Figures 1–3) and in the real data example (Figure S2), TI increases faster than CE. Again consistently with previous results, when temporal order of vectors is shuffled, TI is not sensitive to trial-to-trial shifts in dynamics.