Epidemic contact tracing via communication traces
- PMID: 24787614
- PMCID: PMC4006791
- DOI: 10.1371/journal.pone.0095133
Epidemic contact tracing via communication traces
Abstract
Traditional contact tracing relies on knowledge of the interpersonal network of physical interactions, where contagious outbreaks propagate. However, due to privacy constraints and noisy data assimilation, this network is generally difficult to reconstruct accurately. Communication traces obtained by mobile phones are known to be good proxies for the physical interaction network, and they may provide a valuable tool for contact tracing. Motivated by this assumption, we propose a model for contact tracing, where an infection is spreading in the physical interpersonal network, which can never be fully recovered; and contact tracing is occurring in a communication network which acts as a proxy for the first. We apply this dual model to a dataset covering 72 students over a 9 month period, for which both the physical interactions as well as the mobile communication traces are known. Our results suggest that a wide range of contact tracing strategies may significantly reduce the final size of the epidemic, by mainly affecting its peak of incidence. However, we find that for low overlap between the face-to-face and communication interaction network, contact tracing is only efficient at the beginning of the outbreak, due to rapidly increasing costs as the epidemic evolves. Overall, contact tracing via mobile phone communication traces may be a viable option to arrest contagious outbreaks.
Conflict of interest statement
Figures
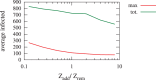
 , while varying the ratio
, while varying the ratio  between the number of removed and added edges. The known network (used for contact tracing) is supposed to be a noisy version of the real network (in which epidemics spread), obtained by removing some edges and adding new ones.
between the number of removed and added edges. The known network (used for contact tracing) is supposed to be a noisy version of the real network (in which epidemics spread), obtained by removing some edges and adding new ones.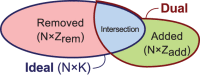
 ,
,  and
and  . The intersection of the two networks, in blue, is of size
. The intersection of the two networks, in blue, is of size  and the union is of size
and the union is of size  .
.

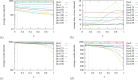
 , with
, with  and
and  . The legend shows the range of contact tracing effort, with
. The legend shows the range of contact tracing effort, with  to
to  . We can see in (a) that contact tracing is effective in reducing the peak number of infected people with
. We can see in (a) that contact tracing is effective in reducing the peak number of infected people with  to
to  times fewer maximum infected cases between
times fewer maximum infected cases between  and
and  . We plot a line at
. We plot a line at  , representing a minimal network overlap which corresponds to the values suggested by the analysis of mobile phone data (see figure 4). The greater the overlap between the tracing and disease spreading networks, the more effective the tracing. At the ideal but unrealistic case of 100% overlap, a
, representing a minimal network overlap which corresponds to the values suggested by the analysis of mobile phone data (see figure 4). The greater the overlap between the tracing and disease spreading networks, the more effective the tracing. At the ideal but unrealistic case of 100% overlap, a  of 2.5 allows to get
of 2.5 allows to get  times fewer maximum infected people in comparison to the case with
times fewer maximum infected people in comparison to the case with  . A low overlap such as
. A low overlap such as  has little effect on the size of the outbreak (the overall number of infected individuals does not decrease much), but still the peak number of infected cases is lowered. With higher overlap, the peak of infections not only decreases in intensity but also gets delayed (c).
has little effect on the size of the outbreak (the overall number of infected individuals does not decrease much), but still the peak number of infected cases is lowered. With higher overlap, the peak of infections not only decreases in intensity but also gets delayed (c).
 and (b) a network overlap of
and (b) a network overlap of  , where
, where  ,
,  ,
,  ,
,  . Contact tracing is always beneficial, even when there is a small overlap between
. Contact tracing is always beneficial, even when there is a small overlap between  and
and  . We observe that contact tracing becomes increasingly effective as the number of infections increases in both network topologies (a) and (b). However, contact tracing becomes decreasingly effective as the number of infections decreases, particularly in the dual network topology case. This can be seen by the worsened effects of the second and sometimes third peaks for the dual network case (e.g., with
. We observe that contact tracing becomes increasingly effective as the number of infections increases in both network topologies (a) and (b). However, contact tracing becomes decreasingly effective as the number of infections decreases, particularly in the dual network topology case. This can be seen by the worsened effects of the second and sometimes third peaks for the dual network case (e.g., with  ).
).
 . The difference in infectious spread over time becomes more apparent in the cases with two peaks, where
. The difference in infectious spread over time becomes more apparent in the cases with two peaks, where  particularly after the second peak, where an increase in network overlap results in fewer infected cases. Note, the log scale employed to make the graphs easily comparable tends to attenuate the differences between curves within a graph.
particularly after the second peak, where an increase in network overlap results in fewer infected cases. Note, the log scale employed to make the graphs easily comparable tends to attenuate the differences between curves within a graph.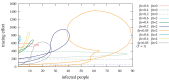
 ) while all other curves are with
) while all other curves are with  .
.
 (left) and
(left) and  (right), when the total tracing effort is constant (400).
(right), when the total tracing effort is constant (400).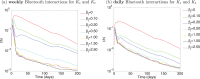
 and
and  . The physical proximity interactions are obtained by the mobile phone Bluetooth data and are incorporated on (a) a weekly scale, and (b) a daily scales.
. The physical proximity interactions are obtained by the mobile phone Bluetooth data and are incorporated on (a) a weekly scale, and (b) a daily scales.
 , phone communication logs are used for tracing,
, phone communication logs are used for tracing,  .
.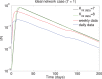
 set to the average daily (and weekly) node degree of the data (see figure S1), but consider a simulated network (labeled as
set to the average daily (and weekly) node degree of the data (see figure S1), but consider a simulated network (labeled as  ). Two data-driven models are considered with the interactions taken from the Bluetooth proximity logs. For all cases,
). Two data-driven models are considered with the interactions taken from the Bluetooth proximity logs. For all cases,  , and therefore
, and therefore  . The real data is considered on weekly and daily scales, and
. The real data is considered on weekly and daily scales, and  are the real physical interactions logged by the community’s Bluetooth sensors.
are the real physical interactions logged by the community’s Bluetooth sensors.References
-
- Holme P, Liljeros F (2013) Beginning and end times of dyadic relationships control disease spreading in empirical contact data. arXiv preprint arXiv: 13076436.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Molecular Biology Databases

