Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennett Reweighting Schemes
- PMID: 24803863
- PMCID: PMC3985817
- DOI: 10.1021/ct401118k
Multiscale Free Energy Simulations: An Efficient Method for Connecting Classical MD Simulations to QM or QM/MM Free Energies Using Non-Boltzmann Bennett Reweighting Schemes
Abstract
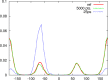
THE RELIABILITY OF FREE ENERGY SIMULATIONS (FES) IS LIMITED BY TWO FACTORS: (a) the need for correct sampling and (b) the accuracy of the computational method employed. Classical methods (e.g., force fields) are typically used for FES and present a myriad of challenges, with parametrization being a principle one. On the other hand, parameter-free quantum mechanical (QM) methods tend to be too computationally expensive for adequate sampling. One widely used approach is a combination of methods, where the free energy difference between the two end states is computed by, e.g., molecular mechanics (MM), and the end states are corrected by more accurate methods, such as QM or hybrid QM/MM techniques. Here we report two new approaches that significantly improve the aforementioned scheme; with a focus on how to compute corrections between, e.g., the MM and the more accurate QM calculations. First, a molecular dynamics trajectory that properly samples relevant conformational degrees of freedom is generated. Next, potential energies of each trajectory frame are generated with a QM or QM/MM Hamiltonian. Free energy differences are then calculated based on the QM or QM/MM energies using either a non-Boltzmann Bennett approach (QM-NBB) or non-Boltzmann free energy perturbation (NB-FEP). Both approaches are applied to calculate relative and absolute solvation free energies in explicit and implicit solvent environments. Solvation free energy differences (relative and absolute) between ethane and methanol in explicit solvent are used as the initial test case for QM-NBB. Next, implicit solvent methods are employed in conjunction with both QM-NBB and NB-FEP to compute absolute solvation free energies for 21 compounds. These compounds range from small molecules such as ethane and methanol to fairly large, flexible solutes, such as triacetyl glycerol. Several technical aspects were investigated. Ultimately some best practices are suggested for improving methods that seek to connect MM to QM (or QM/MM) levels of theory in FES.
Figures

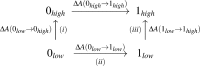


Similar articles
-
Comparison of Methods To Reweight from Classical Molecular Simulations to QM/MM Potentials.J Chem Theory Comput. 2016 Apr 12;12(4):1466-80. doi: 10.1021/acs.jctc.5b01188. Epub 2016 Mar 23. J Chem Theory Comput. 2016. PMID: 26928941 Free PMC article.
-
Efficiently computing pathway free energies: New approaches based on chain-of-replica and Non-Boltzmann Bennett reweighting schemes.Biochim Biophys Acta. 2015 May;1850(5):944-953. doi: 10.1016/j.bbagen.2014.09.016. Epub 2014 Sep 17. Biochim Biophys Acta. 2015. PMID: 25239198
-
Computation of Hydration Free Energies Using the Multiple Environment Single System Quantum Mechanical/Molecular Mechanical Method.J Chem Theory Comput. 2016 Jan 12;12(1):332-44. doi: 10.1021/acs.jctc.5b00874. Epub 2015 Dec 11. J Chem Theory Comput. 2016. PMID: 26613419 Free PMC article.
-
Progress in ab initio QM/MM free-energy simulations of electrostatic energies in proteins: accelerated QM/MM studies of pKa, redox reactions and solvation free energies.J Phys Chem B. 2009 Feb 5;113(5):1253-72. doi: 10.1021/jp8071712. J Phys Chem B. 2009. PMID: 19055405 Free PMC article. Review.
-
Advances in binding free energies calculations: QM/MM-based free energy perturbation method for drug design.Curr Pharm Des. 2013;19(26):4674-86. doi: 10.2174/1381612811319260002. Curr Pharm Des. 2013. PMID: 23260025 Review.
Cited by
-
Calculating distribution coefficients based on multi-scale free energy simulations: an evaluation of MM and QM/MM explicit solvent simulations of water-cyclohexane transfer in the SAMPL5 challenge.J Comput Aided Mol Des. 2016 Nov;30(11):989-1006. doi: 10.1007/s10822-016-9936-x. Epub 2016 Aug 30. J Comput Aided Mol Des. 2016. PMID: 27577746
-
Multiple environment single system quantum mechanical/molecular mechanical (MESS-QM/MM) calculations. 1. Estimation of polarization energies.J Phys Chem A. 2015 Mar 5;119(9):1511-23. doi: 10.1021/jp5072296. Epub 2014 Oct 30. J Phys Chem A. 2015. PMID: 25321186 Free PMC article.
-
Quantum mechanical force fields for condensed phase molecular simulations.J Phys Condens Matter. 2017 Sep 27;29(38):383002. doi: 10.1088/1361-648X/aa7c5c. Epub 2017 Aug 17. J Phys Condens Matter. 2017. PMID: 28817382 Free PMC article.
-
Effect of set up protocols on the accuracy of alchemical free energy calculation over a set of ACK1 inhibitors.PLoS One. 2019 Mar 12;14(3):e0213217. doi: 10.1371/journal.pone.0213217. eCollection 2019. PLoS One. 2019. PMID: 30861030 Free PMC article.
-
CHARMM at 45: Enhancements in Accessibility, Functionality, and Speed.J Phys Chem B. 2024 Oct 17;128(41):9976-10042. doi: 10.1021/acs.jpcb.4c04100. Epub 2024 Sep 20. J Phys Chem B. 2024. PMID: 39303207 Free PMC article. Review.
References
-
- Shirts M. R.; Mobley D. L.; Chodera J. D.; Pande V. S. Accurate and efficient corrections for missing dispersion interactions in molecular simulations. J. Phys. Chem. B 2007, 111, 13052–13063. - PubMed
-
- de Ruiter A.; Oostenbrink C. Efficient and Accurate Free Energy Calculations on Trypsin Inhibitors. J. Chem. Theory Comput. 2012, 8, 3686–3695. - PubMed
-
- de Ruiter A.; Boresch S.; Oostenbrink C. Comparison of thermodynamic integration and Bennett’s acceptance ratio for calculating relative protein-ligand binding free energies. J. Comput. Chem. 2013, 34, 1024–1034. - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials
Miscellaneous
