Through the eyes of a bird: modelling visually guided obstacle flight

Abstract

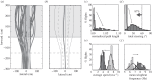
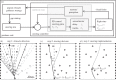
Various flight navigation strategies for birds have been identified at the large spatial scales of migratory and homing behaviours. However, relatively little is known about close-range obstacle negotiation through cluttered environments. To examine obstacle flight guidance, we tracked pigeons (Columba livia) flying through an artificial forest of vertical poles. Interestingly, pigeons adjusted their flight path only approximately 1.5 m from the forest entry, suggesting a reactive mode of path planning. Combining flight trajectories with obstacle pole positions, we reconstructed the visual experience of the pigeons throughout obstacle flights. Assuming proportional-derivative control with a constant delay, we searched the relevant parameter space of steering gains and visuomotor delays that best explained the observed steering. We found that a pigeon's steering resembles proportional control driven by the error angle between the flight direction and the desired opening, or gap, between obstacles. Using this pigeon steering controller, we simulated obstacle flights and showed that pigeons do not simply steer to the nearest opening in the direction of flight or destination. Pigeons bias their flight direction towards larger visual gaps when making fast steering decisions. The proposed behavioural modelling method converts the obstacle avoidance behaviour into a (piecewise) target-aiming behaviour, which is better defined and understood. This study demonstrates how such an approach decomposes open-loop free-flight behaviours into components that can be independently evaluated.

Keywords: flight guidance; obstacle negotiation; path planning; pigeon flight; proportional–derivative controller.

Figure 1.

Obstacle avoidance flight corridor and motion tracking. (a) Pigeons were trained to fly between two perches located at either end of a 20 m indoor flight corridor. An obstacle ‘pole forest’ was erected 10 m from the take-off perch to elicit obstacle negotiation. Five high-speed cameras captured the flight trajectories (green section) throughout the entire obstacle forest, including 5 m of the approach. (b) Starting from a standard grid (red dots), for each flight obstacles were randomly assigned one of five positions (the grid centre) or one of four orthogonal locations 25 cm from the grid centre (illustrated by red arrows). (c) Four 2.4 mm LEDs were attached to each pigeon in combination with a small battery-pack (16.5 g total) to facilitate positional tracking of the head and body. (d) Three-dimensional flight trajectories were reconstructed from the high-speed videos. An example trajectory (green trace) is marked every 200 ms (blue circles). To model steering through the obstacle field, we considered a section of the flight from 50 cm in front of the obstacle field to 20 cm before the pigeon left the obstacle field (blue arrow). (e) Three-dimensional head positions and pole distributions were used to reconstruct the in-flight visual motion of obstacles with respect to the pigeon's head (and eyes). The modelling process assumed that pigeons always aimed towards visual centres of gaps.

Figure 2.

Characteristics of pigeon obstacle flight. (a) The pigeons flew straight, close to the corridor midline in the absence of obstacles (light grey traces). When challenged with obstacles (dark grey traces), flight trajectories diverged within the obstacle field. (b) Steering was first observed 1.5 m in advance of obstacles, determined when the standard deviation (dark grey dash lines) and the limit (dark grey solid lines) exceeded control trajectories (light grey dash lines and solid lines). (c) Flight trajectories without obstacles were extremely straight over the 6 m calibrated section of the flight corridor, with a normalized path length of 1.00 + 0.002. Obstacle flights were slightly longer, with a normalized path length of 1.03 ± 0.025. The path length was normalized to the straight-line reference. (d) Control flights normally contained less than 5° of total steering; whereas obstacle flights involved total steering summing up to approximately 80°. However, 87% of obstacle flights contained less than 60° of total steering (thick arrow). (e) Flight speed was reduced 44.5% from 6.95 ± 0.64 m s⁻¹ to 3.86 ± 0.52 m s⁻¹, and wingbeat frequency (f) increased by approximately 21% from 6.58 ± 0.63 Hz to 7.95 ± 0.59 Hz when pigeons flew through the obstacles.

Figure 3.

Modelling framework for pigeon obstacle negotiation. (a) The pigeon's obstacle negotiation is expressed as a feedback control system with a steering controller embedded within a guidance rule (gap selection). The model determines a steering aim at each time step based on a guidance rule. Gap-aiming behaviour suggests that this aim is represented by one of the available gaps in the obstacle field, which then becomes the reference for the steering controller. The steering controller subsequently generates a steering command based on a given set of proportional and derivative gains. After a given visuomotor delay, the steering is implemented under the influence of steering inertia. (b–d) The obstacle navigation behaviour can be broken down into three subsequent steps: obstacle detection, steering decision and steering implementation. (b) For each time step, relevant obstacles are identified within a given attention zone, establishing the available gaps (dashed lines). The model pigeon focuses on those that fall within ± 30° of the flight direction, which the model considers its ‘attention zone’ (solid lines; see text for details). The side-walls were modelled as very dense rows of obstacles (black squares). (c) Depending on the guidance rule, one of the available gaps is selected as the steering aim. The deviation angle θ and its derivative are calculated based on flight direction and the steering aim. (d) The steering controller determines the amount of steering that occurs after the visuomotor delay τ_d.

Figure 4.

Pigeons bias their flight paths towards largest gaps. (a) Based on the gap-aiming paradigm, we proposed three potential guidance rules: (1) steer to the gap closest to the destination direction (red), (2) steer to the gap in the existing flight direction (magenta) or (3) steer to the largest visual gap (blue). (b) To establish a reference for our gap-aiming paradigm, we reconstructed a conventional obstacle repellence model with a variable range attention zone (marked by dashed lines), in which the repellent effects from all obstacles within that threshold range and angle were summed. (c) To provide the simulations with more realistic sensory information, we incorporated sensory uncertainty by assuming a Gaussian distribution centred at each obstacle position for the model to sample from. The standard deviation of this Gaussian distribution was varied to test each steering strategy across a range of noise levels. (d) We simulated 40 pigeon flights (not used for steering controller tuning) given only the initial conditions (i.e. body position, flight direction, entry speed) 0.5 m before the obstacle field. Some simulations recapitulated the observed flight trajectories (blue trace) and some did not (green trace). We quantified the percentage of flight trajectory matches for each guidance rule in each simulation set (40 flights). To examine the effect of sensory uncertainty, we ran each simulation set 100 times under each sensory uncertainty condition. (e) We varied the threshold range of the obstacle repellence model and found that a threshold of 0.5 m yielded the greatest mean predictive power of 58% with zero noise (solid blue line). The corresponding maximum predictive power (blue dashed line) reached 64% at 6° sensory uncertainty. The obstacle repellence model's predictive power was lower when reacting to the obstacles too late (less than 0.25 m) or too early (less than 1 m). (f) The gap-aiming navigational paradigm requires that pigeons always aim to a gap between two obstacles. In this set of simulations, the modelled pigeon randomly aims to a gap over a given angular size threshold. As the threshold increases, the predictive power increases for sensory uncertainty ranging from 0 to 20°, signifying the importance of gap size in the decision-making process. (g) Maintaining the gap size threshold at 5°, we ran simulations using the three basic guidance rules described in (a). The destination gap rule and flight direction gap rule both underperformed compared with random gap selection as in (f). The maximum predictive power of those simulations where the model pigeons aimed for the largest visual gap, however, approached 80% around a noise level of 6°, outperforming the alternative gap selection rules, random gap selection (f) and the obstacle repellence model (e).

Figure 5.

Steering controller tuning. Tuning was based on the average deviation between model-predicted and observed flight directions, determined every 10 ms time step for the best steering aim, for all possible combinations of gains and delay, and for all obstacle flights. To make the flight controller independent of the guidance rule, the tuning process assumed that the pigeon always aimed to one of the available gaps without imposing an a priori rule on gap selection, but instead selected the gap that resulted in the best fit with the observed flight path. The proportional controller was broadly tuned with a minimum deviation band centred about a gain of approximately 4 s⁻¹ (column 1). For the derivative control, however, a visuomotor delay of approximately 130 ms was strongly selected but with a broadly tuned derivative gain (column 2). We implemented steering inertia as a stabilizing term. The stabilization gain is, by definition, negative and is generally quite small (column 3). We extracted the controller parameters that provided the best fit to the observed data; these are presented in table 1 (see text for details). We then demonstrated that pigeon obstacle flights can be modelled as aiming to a gap by regressing the observed angular rate of change of flight direction against that predicted by the best fitting controller parameters. The steering controller predicted the observed steering extremely well (R² = 0.97 for all four cases; column 4), under the paradigm of gap aiming. (Online version in colour.)