Predicting and correcting ataxia using a model of cerebellar function
- PMID: 24812203
- PMCID: PMC4065021
- DOI: 10.1093/brain/awu115
Predicting and correcting ataxia using a model of cerebellar function
Abstract
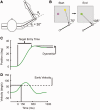
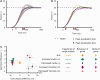
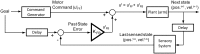
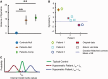
Cerebellar damage results in uncoordinated, variable and dysmetric movements known as ataxia. Here we show that we can reliably model single-joint reaching trajectories of patients (n = 10), reproduce patient-like deficits in the behaviour of controls (n = 11), and apply patient-specific compensations that improve reaching accuracy (P < 0.02). Our approach was motivated by the theory that the cerebellum is essential for updating and/or storing an internal dynamic model that relates motor commands to changes in body state (e.g. arm position and velocity). We hypothesized that cerebellar damage causes a mismatch between the brain's modelled dynamics and the actual body dynamics, resulting in ataxia. We used both behavioural and computational approaches to demonstrate that specific cerebellar patient deficits result from biased internal models. Our results strongly support the idea that an intact cerebellum is critical for maintaining accurate internal models of dynamics. Importantly, we demonstrate how subject-specific compensation can improve movement in cerebellar patients, who are notoriously unresponsive to treatment.
Keywords: ataxia; cerebellum; computational model; dysmetria; internal model.
© The Author (2014). Published by Oxford University Press on behalf of the Guarantors of Brain. All rights reserved. For Permissions, please email: journals.permissions@oup.com.
Figures



References
-
- Angel RW. Barognosis in a patient with hemiataxia. Ann Neurol. 1980;7:73–7. - PubMed
-
- Bastian AJ. Learning to predict the future: the cerebellum adapts feedforward movement control. Curr Opin Neurobiol. 2006;16:645–9. - PubMed
-
- Bastian AJ, Martin TA, Keating JG, Thach WT. Cerebellar ataxia: abnormal control of interaction torques across multiple joints. J Neurophysiol. 1996;76:492–509. - PubMed
-
- Bastian AJ, Zackowski KM, Thach WT. Cerebellar ataxia: torque deficiency or torque mismatch between joints? J Neurophysiol. 2000;83:3019–30. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

