A Brief Review: The Z-curve Theory and its Application in Genome Analysis

Abstract

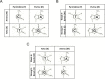
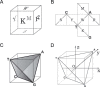
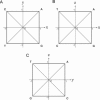
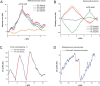
In theoretical physics, there exist two basic mathematical approaches, algebraic and geometrical methods, which, in most cases, are complementary. In the area of genome sequence analysis, however, algebraic approaches have been widely used, while geometrical approaches have been less explored for a long time. The Z-curve theory is a geometrical approach to genome analysis. The Z-curve is a three-dimensional curve that represents a given DNA sequence in the sense that each can be uniquely reconstructed given the other. The Z-curve, therefore, contains all the information that the corresponding DNA sequence carries. The analysis of a DNA sequence can then be performed through studying the corresponding Z-curve. The Z-curve method has found applications in a wide range of areas in the past two decades, including the identifications of protein-coding genes, replication origins, horizontally-transferred genomic islands, promoters, translational start sides and isochores, as well as studies on phylogenetics, genome visualization and comparative genomics. Here, we review the progress of Z-curve studies from aspects of both theory and applications in genome analysis.

Keywords: GC profile; Gene finding; Genomic island; Replication origin; Z-curve..

Fig. (1)

Chemical structures of four DNA bases, displaying the basic symmetry.

Fig. (2)

The coordinate system based on the regular tetrahedron. A) a cube displaying the basic symmetry: R/Y, M/K and S/W symmetry; B) an extended plot for the cube. C) a cube and its inscribed tetrahedron; D) a coordinate system is set up to establish the Z-curve theory.

Fig. (3)

Projection of the 3-D coordinates onto planes. The projection of the 3-D coordinate system onto the A) x-y, B) x-z and C) y-z planes.

Fig. (4)

The Z-curve reveals features of archaeal, bacterial and eukaryotic genomes. The Z-curve shows replication origins in genomes of A) the archaeon Methanosarcina mazei Tuc01 and B) the bacterium Salmonella enterica subsp. Typhi str. CT18. The Z-curve shows C) the domain structure in chromosome 11 of finch, and D) horizontally-transferred genomic elements in the genome of Streptococcus pneumoniae ATCC 700669.

Fig. (5)

Genomic nucleotide composition features revealed by the Z-curve method. 3-D Z-curves for human chromosome 6 (A) and chimpanzee chromosome 6 (B). The 2 homologous chromosomes show similar Z-curves. To show global nucleotide composition patterns, Z-curves have been smoothed for 50,000 times by using the B-spline function. An ORF-flower phenomenon is revealed by the Z-curve method in genomes with high GC content. All open reading frames are mapped onto a 9-dimensional space using the Z-curve method, and protein-coding ORFs are located in a distinct region, compared with non-coding ORFs and intergenic sequences. Shown are principal component analysis for the genomes of Ralstonia solanacearum GMI1000 (C) and Streptomyces avermitilis MA 4680 (D). F0, F1, F2, R0, R1, and R2 stand for reading frames of protein-coding, forward 1, forward 2, non-coding reverse 0, reverse 1 and reverse 2, respectively.