The effect of seasonal birth pulses on pathogen persistence in wild mammal populations

Abstract

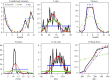
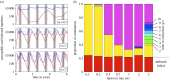
The notion of a critical community size (CCS), or population size that is likely to result in long-term persistence of a communicable disease, has been developed based on the empirical observations of acute immunizing infections in human populations, and extended for use in wildlife populations. Seasonal birth pulses are frequently observed in wildlife and are expected to impact infection dynamics, yet their effect on pathogen persistence and CCS have not been considered. To investigate this issue theoretically, we use stochastic epidemiological models to ask how host life-history traits and infection parameters interact to determine pathogen persistence within a closed population. We fit seasonal birth pulse models to data from diverse mammalian species in order to identify realistic parameter ranges. When varying the synchrony of the birth pulse with all other parameters being constant, our model predicted that the CCS can vary by more than two orders of magnitude. Tighter birth pulses tended to drive pathogen extinction by creating large amplitude oscillations in prevalence, especially with high demographic turnover and short infectious periods. Parameters affecting the relative timing of the epidemic and birth pulse peaks determined the intensity and direction of the effect of pre-existing immunity in the population on the pathogen's ability to persist beyond the initial epidemic following its introduction.

Keywords: birth pulse; critical community size; seasonality; stochastic model; wildlife epidemiology.

Figure 1.

Observed and predicted births for six datasets. Black solid lines show data (numbers of births, except dataset 13: proportion of females with pups); coloured symbols show the three fitted models. Numbers preceding common names refer to datasets listed in the electronic supplementary material, table S1.

Figure 2.

Effect of various parameters on the dynamics and persistence of infection. Contour plots show probability of pathogen extinctions within 10 years of introduction (conditional on successful invasion) as a function of average population size (ν) according to the scale in (a). The black line shows the CCS, defined as the population size resulting in 50% of pathogen extinction within 10 years. For each combination of parameter values, 1000 stochastic simulations were run. Line plots show deterministic dynamics, with the numbers of susceptible S(t) in blue and infected I(t) in red; the dashed line shows the threshold value N(t)/R₀ for the number of susceptible individuals over which the infection spreads (dI/dt > 0); the width of the shaded vertical bars reflects the duration and intensity of seasonal births, B(t). (a) Effect of the turnover rate (m) and recovery rate (γ) in a population with a constant birth rate (s = 0). Parameter values: γ = 12 yr⁻¹ (left), m = 1 yr⁻¹ (right), R₀ = 4, φ = 0. (b) Effect of synchrony parameter s. Parameter values: m = 1 yr⁻¹, γ = 12 yr⁻¹, R₀ = 4, φ = 0. (c,d) Effect of prior immunity (p), comparing no prior immunity (left) with 50% of the population initially immune (right). Inset labels (i–iv) show the combinations of parameter values used in the corresponding deterministic plots. Parameter values: (c) s = 10, m = 0.1 yr⁻¹, γ = 6 yr⁻¹, R₀ = 4; (d) s = 10, m = 0.5 yr⁻¹, γ = 12 yr⁻¹, R₀ = 4. An increase in p can shift the epidemic peak closer to the next birth pulse and rescue the pathogen (c) or on the contrary, shift the epidemic peak from before the birth pulse to after it, resulting in deeper post-epidemic trough (d). (e) Effect of the phase of the birth pulse (φ). The three values of φ (−π/3, 0 and π/6) shown correspond to lags of two, six and 10 months from time of pathogen introduction until the next birth pulse peak. Parameter values: s = 10, m = 0.5 yr⁻¹, γ = 12 yr⁻¹, R₀ = 4.

Figure 3.

Effect of turnover rate m on the dynamics and persistence of infection with a birth pulse s = 10. (a) Deterministic dynamics for three values of m (0.2, 1 and 3 yr⁻¹ from top to bottom), with the numbers of susceptible S(t) in blue and infected I(t) in red; the dashed line shows the threshold value N(t)/R₀ for the number of susceptible individuals over which the infection spreads (dI/dt > 0); the width of the shaded vertical bars reflects the duration and intensity of seasonal births, B(t). (b) Stacked histograms of time to pathogen extinction in seven series of 1000 stochastic simulations run for 10 years, with increasing values of m along the horizontal axis. Red bars show the proportion of simulations with no outbreak (extinction after fewer than five infection events). Parameter values: s = 10, γ = 12 yr⁻¹, R₀ = 4, ν = 50 000.