Revised Backbone-Virtual-Bond-Angle Potentials to Treat the l- and d-Amino Acid Residues in the Coarse-Grained United Residue (UNRES) Force Field

Abstract

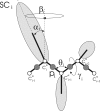
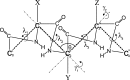
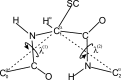
Continuing our effort to introduce d-amino-acid residues in the united residue (UNRES) force field developed in our laboratory, in this work the C^α ··· C^α ··· C^α backbone-virtual-bond-valence-angle (θ) potentials for systems containing d-amino-acid residues have been developed. The potentials were determined by integrating the combined energy surfaces of all possible triplets of terminally blocked glycine, alanine, and proline obtained with ab initio molecular quantum mechanics at the MP2/6-31G(d,p) level to calculate the corresponding potentials of mean force (PMFs). Subsequently, analytical expressions were fitted to the PMFs to give the virtual-bond-valence potentials to be used in UNRES. Alanine represented all types of amino-acid residues except glycine and proline. The blocking groups were either the N-acetyl and N',N'-dimethyl or N-acetyl and pyrrolidyl group, depending on whether the residue next in sequence was an alanine-type or a proline residue. A total of 126 potentials (63 symmetry-unrelated potentials for each set of terminally blocking groups) were determined. Together with the torsional, double-torsional, and side-chain-rotamer potentials for polypeptide chains containing d-amino-acid residues determined in our earlier work (Sieradzan et al. J. Chem. Theory Comput., 2012, 8, 4746), the new virtual-bond-angle (θ) potentials now constitute the complete set of physics-based potentials with which to run coarse-grained simulations of systems containing d-amino-acid residues. The ability of the extended UNRES force field to reproduce thermodynamics of polypeptide systems with d-amino-acid residues was tested by comparing the experimentally measured and the calculated free energies of helix formation of model KLALKLALxxLKLALKLA peptides, where x denotes any d- or l- amino-acid residue. The obtained results demonstrate that the UNRES force field with the new potentials reproduce the changes of free energies of helix formation upon d-substitution but overestimate the free energies of helix formation. To test the ability of UNRES with the new potentials to reproduce the structures of polypeptides with d-amino-acid residues, an ab initio replica-exchange folding simulation of thurincin H from Bacillus thuringiensis, which has d-amino-acid residues in the sequence, was carried out. UNRES was able to locate the native α-helical hairpin structure as the dominant structure even though no native sulfide-carbon bonds were present in the simulation.

Figure 1

UNRES model of polypeptide chains. The interaction sites are peptide-group centers (p), and side-chain centers (SC) attached to the corresponding α-carbons with different C^α ··· SC bond lengths, d_SC. The peptide groups are represented as dark gray circles and the side chains are represented as light gray ellipsoids of different size. The α-carbon atoms are represented by small open circles. The geometry of the chain can be described either by the virtual-bond vectors dC_i (from C_i^α to C_i+1^α), i = 1,2,...,n – 1, and dX_i (from C_i^α to SC_i), i = 2,...,n – 1, represented by thick lines, where n is the number of residues, or in terms of virtual-bond lengths, backbone virtual-bond angles θ_i, i = 1,2,...,n – 2, backbone virtual-bond-dihedral angles γ_i, i = 1,2,...,n – 3, and the angles α_i and β_i,i = 2,3,...,n – 1 that describe the location of a side chain with respect to the coordinate frame defined by C_i–1^α, C_i^α, and C_i^α, C_i+1^α.

Figure 2

Illustration of the model terminally blocked tripeptides constructed to compute the integrals of eqs 3. Each X, Y, and Z denotes side-chains of l-Ala, d-Ala, Gly, l-Pro, or d-Pro.

Figure 3

Definition of the dihedral angles λ⁽¹⁾ and λ⁽²⁾ for rotation of a peptide unit about the C^α ··· C^α virtual bonds of a peptide unit.

Figure 4

Sample contour plots of the valence bond bending potentials U_{l–Ala–(d,l)–Ala–(d,l)–Ala–NHMe}(θ, γ⁽¹⁾, γ⁽²⁾) as functions of θ and γ⁽²⁾ angles for alanine-type tripeptides with NHMe terminal groups, where (d,l)-Ala indicates a d- or an l-Ala residue, for three selected values of the γ⁽¹⁾ angle =60°, 180°, −60°. γ₁ is always fixed and its value is printed at the top of each panel; γ₂ is a variable. Finally, the energy scale (kcal/mol) is on the top of the figure.

Figure 5

Same as Figure 4, but for (d,l)-Ala-Pir.

Figure 6

(A) Model 1 from the ensemble of NMR structures of thurincin H (PDB code: 2LBZ); black lines mark the sulfide (S–C^α) bonds, (B) the calculated structure of thurincin H with the lowest C^αRMSD (3.86 Å) obtained from the MREMD simulation, and (C) average structure of the top cluster of the calculated structures of thurincin H at 310 K; C^α-RMSD from the NMR Model 1 structure is 5.72 Å.