Structural basis for the nonlinear mechanics of fibrin networks under compression

Abstract

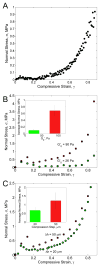
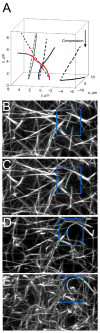
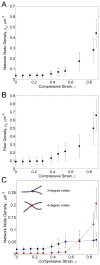
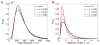
Fibrin is a protein polymer that forms a 3D filamentous network, a major structural component of protective physiological blood clots as well as life threatening pathological thrombi. It plays an important role in wound healing, tissue regeneration and is widely employed in surgery as a sealant and in tissue engineering as a scaffold. The goal of this study was to establish correlations between structural changes and mechanical responses of fibrin networks exposed to compressive loads. Rheological measurements revealed nonlinear changes of fibrin network viscoelastic properties under dynamic compression, resulting in network softening followed by its dramatic hardening. Repeated compression/decompression enhanced fibrin clot stiffening. Combining fibrin network rheology with simultaneous confocal microscopy provided direct evidence of structural modulations underlying nonlinear viscoelasticity of compressed fibrin networks. Fibrin clot softening in response to compression strongly correlated with fiber buckling and bending, while hardening was associated with fibrin network densification. Our results suggest a complex interplay of entropic and enthalpic mechanisms accompanying structural changes and accounting for the nonlinear mechanical response in fibrin networks undergoing compressive deformations. These findings provide new insight into the fibrin clot structural mechanics and can be useful for designing fibrin-based biomaterials with modulated viscoelastic properties.

Keywords: Compression; Confocal microscopy; Fibrin networks; Mechanical response; Network structure; Rheology.

Figure 1

Experimental setup combining rheometry and confocal microscopy to measure structural mechanics of human plasma fibrin clots. Rheological and structural data were simultaneously collected and stored independently by the coupled systems of data acquisition.

Figure 2

(A) Relative elastic and loss moduli, G′* and G″*, respectively, as a function of compressive strain. Here, G′* = G′/G′₀ and G″* = G″/G″₀, where G′₀ and G″₀ are the initial elastic and loss moduli of uncompressed clots, while G′ and G″ comprise the elastic and loss moduli, respectively, at different degrees of compression. The inset figure represents the relative moduli-compressive strain dependence in a semi-logarithmic scale for compressive strains from γ = 0.75 to γ = 0.9. (B) A measure of the viscosity/elasticity ratio of fibrin clots, the relative phase angle, δ* = δ/ δ₀, as a function of compressive strain γ, where δ = atan(G″/G′) for the compressed and δ₀ = atan(G″₀/G′₀) for the uncompressed clots, respectively (M±SD). Each plot shown in Figure 2 is averaged over 3 fibrin clot samples prepared under the same conditions and having very similar initial values of G′₀ and G″₀ (M±SD).

Figure 3

(A) Normal stress, σ, as a function of compressive strain, γ, of fibrin clots corresponding to the changes in viscoelasticity shown in Figure 2. (B) Normal stress, σ, as a function of compressive strain, γ, for two different fibrin clots with the initial elasticity (G′₀) of 26 and 90 Pa. The inset bars show the mean normal stress values for the clots with two different G′₀ values averaged over compressive strains from γ = 0.4 to γ = 0.6 (n=4). (C) Normal stress, σ, as a function of compressive strain (γ) for two different compression steps (Δh) of 20 and 50 μm. The inset bars show the mean normal stress values for two compression steps averaged over compressive strains from γ = 0.4 to γ = 0.6 (M±SD, n=4).

Figure 4

Fibrin clot pre-compression/decompression/recompression cycles performed for different decompression amplitudes and for various degrees of clot pre-compression, D. Here, D = L₀/L_PC, where L₀ and L_PC are the thickness dimensions of uncompressed and pre-compressed clots, respectively. The relative elastic modulus of fibrin networks (A) as a function of decompressive strain, γ*, and (B) as a function of shifted (normalized) decompressive strain (γ**). The different pre-compression degrees are shown by different colors and symbols (upper right inset key). Arrows show the directions of decompression and re-compression in a single cycle. Figure B, left inset, shows the relative elastic modulus, G′**, non-dimensionalized with respect to fibrin clot pre-compression thickness in each cycle, versus shifted (normalized) strain γ**. The arrows show direction of decompression stiffening for different cycles.

Figure 5

(A) Examples of fiber buckling and bending in Z direction as a result of the fibrin network vertical compression. Four reconstructed individual fibers from different parts of the network are shown in different colors before (γ = 0, dashed lines) and after (γ = 0.33, solid lines) the compression. (B–E) Structural changes of a fibrin network under compression shown as a z-projection of confocal images of the network z-stack for different compressive strains: γ = 0 (B), γ = 0.18 (C), γ = 0.38 (D), and γ = 0.53 (E). The blue boxes highlight an individual fiber experiencing a progressive buckling and bending deformations. As the degree of network compression increases, the individual fiber appears increasingly bent and the entire network becomes denser. All images are x-y projections of z-stack images of a clot volume of 35.8 × 35.8 × 25.5 μm.

Figure 6

Fraction of bent fibers and their segments, α_b, and the fiber bending degree, χ, as a function of compressive strain γ. Here, α_b is defined as the ratio of the number of bent fibers to the total number of fibers analyzed, and χ = l_c/l_f, where l_c is a fiber contour length and l_f is the shortest distance between the fiber end-nodes.

Figure 7

Densification of the fibrin network upon compression. (A) Fibrin network node density, ρ_n, and (B) fibrin network fiber density, ρ_f, as a function of compressive strain, γ, (M±SD, n = 3). (C) Increasing branching in the fibrin network upon compression. 3-degree (circles) and 4-degree (squares) node densities in fibrin networks as a function of compressive strain. The corresponding types of fiber connectivity are schematically shown.

Figure 8

Fibrin fiber diameter (A) and fibrin network segment length (B) probability distribution functions, P_n(d) and P_n(L), for various applied compressive strains, γ. Fiber length histograms and length distributions of three- and four-degree connectivity fibers and are provided in Figure S6 and Figure S7 in Supplementary Information.

Figure 9

The stress-softening in fibrin networks exposed to compression can originate from fiber buckling and bending shown here schematically (A→B). Stress-hardening can arise owing to fiber resisting extension and buckling of filaments resisting normal compression as well as due to densification of the network resulting in the increase of criss-crossing fibers (B→C). Here, σ is the normal compression stress, γ is the compression strain, and γ′ is the compression strain characterizing softening-hardening transition.