A computational model for the loss of neuronal organization in microcolumns

Abstract

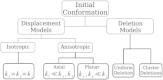
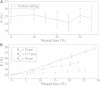
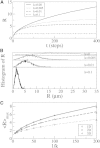
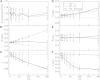
A population of neurons in the cerebral cortex of humans and other mammals organize themselves into vertical microcolumns perpendicular to the pial surface. Anatomical changes to these microcolumns have been correlated with neurological diseases and normal aging; in particular, in area 46 of the rhesus monkey brain, the strength of microcolumns was shown to decrease with age. These changes can be caused by alterations in the spatial distribution of the neurons in microcolumns and/or neuronal loss. Using a three-dimensional computational model of neuronal arrangements derived from thin tissue sections and validated in brain tissue from rhesus monkeys, we show that neuronal loss is inconsistent with the findings in aged individuals. In contrast, a model of simple random neuronal displacements, constrained in magnitude by restorative harmonic forces, is consistent with observed changes and provides mechanistic insights into the age-induced loss of microcolumnar structure. Connection of the model to normal aging and disease are discussed.

Figure 1

Schematic diagram of the different models and their mechanisms for neuronal displacement and deletion. The bottom row of the diagram represents the specific mechanisms of the respective models. The unrestricted displacement model is not shown.

Figure 2

Typical 3D representations of neuronal ensembles resulting from the different displacement and deletion mechanisms. For clarity, the neurons, represented by bright small spheres, are those within a thin section obtained from the middle region of a larger cubic ensemble box. (A) Neuronal positions correspond to the original unaltered ensemble (healthy brains). (B) The same configuration as seen from the top, with arrows indicating representative microcolumns (microcolumns oriented along the axis coming out of the page). (C) A typical neuronal ensemble resulting from the harmonic force displacement mechanism using the smallest force constant (k = 0.005). (D–F) The neuronal-deletion mechanisms acting on the original ensemble from A, with uniform deletions corresponding to a maximum of ∼35% neuronal loss (D), and deletions of clusters of radius 20 μm (E) and 50 μm (F) corresponding to neuronal losses of ∼20% and ∼18%, respectively.

Figure 3

Percentage strength of microcolumns for the neuronal deletion mechanisms. (A) F is shown as a function of the percentage of neuronal loss where individual neurons were deleted at random. (B) F is shown as a function of total neuronal loss for the cases of neuronal cluster deletions within a sphere of radius R_cl.

Figure 4

(A) R(t) for one realization of a neuronal system undergoing random displacements (symmetric in all axes) with a harmonic restorative force for a selection of spring constant values. Systems with no restorative force (k = 0) exhibited an R value that increased without bounds. At equilibrium, R for systems with nonzero values of k reached a maximum average, <R>_max. See the Supporting Material for details of how to determine the critical number of time steps needed for convergence. (B) Histograms of R from individual neurons of the realizations shown in A, where the histogram for the spring constant value of k = 0 was calculated at t = 1000 and those for values of k > 0 at the equilibrium, <R>_max. (C) <R>_max as a function of 1/k ( symbols, taken from simulations) and k_x, k_y, and k_z (solid lines, from Eq. A16 in the Supporting Material).

Figure 5

Percentage strength of microcolumns, F, for the harmonic force displacement mechanisms. (A) Percentage strength of microcolumns as a function of 1/k for different neuronal displacement mechanisms. (B) Percentage strength of microcolumns as a function of <R>_max for different neuronal displacement mechanisms.

Figure 6

Microcolumnar measurements of neuronal systems undergoing different harmonic-force neuronal displacement mechanisms as a function of 1/k. The graphs correspond to neuronal density, ρ (A), width, W (B), degree of microcolumnar periodicity, T (C), interneuronal distance of microcolumns, Y (D), intercolumn distance, P (E), and length, L (F).