Extortion subdues human players but is finally punished in the prisoner's dilemma

Abstract

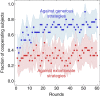
Extortion is the practice of obtaining advantages through explicit forces and threats. Recently, it was demonstrated that even the repeated prisoner's dilemma, one of the key models to explain mutual cooperation, allows for implicit forms of extortion. According to the theory, extortioners demand and receive an excessive share of any surplus, which allows them to outperform any adapting co-player. To explore the performance of such strategies against humans, we have designed an economic experiment in which participants were matched either with an extortioner or with a generous co-player. Although extortioners succeeded against each of their human opponents, extortion resulted in lower payoffs than generosity. Human subjects showed a strong concern for fairness: they punished extortion by refusing to fully cooperate, thereby reducing their own, and even more so, the extortioner's gains. Thus, the prospects of extorting others in social relationships seem limited; in the long run, generosity is more profitable.

Figure 1. Average payoffs across the four treatments for humans (empty bars) and the ZD strategies implemented by the computer programme (filled bars).

In line with the theory, extortioners succeed against their human co-players, whereas generous ZD strategies lag behind their human opponents. Throughout the paper, we use two-tailed non-parametric tests for our statistical analysis, with each iterated game between a human co-player and the computer as our statistical unit (thus we have 16 independent observations for each of the 2 strong treatments, and 14 independent observations for each of the 2 weak treatments). In the above graph, three stars indicate significance at the level α=0.001, and one star means significance for α=0.05 (using Wilcoxon matched-pairs signed-rank tests with n_ES=n_GS=16, n_EM=n_GM=14). As an auxiliary information, we also provide error bars indicating the 95% confidence interval. Individual results for all 60 individuals are presented in the Supplementary Table 1.

Figure 2. Comparison of experimental results to the theoretical prediction.

The grey-shaded area depicts the space of possible payoffs for the two players, that is, the ZD strategy implemented by the computer programme (x axis) and the human co-player (y axis). The black line corresponds to the theoretical prediction for the expected payoffs (as explained in the Methods) and the open circles indicate the outcome of the experiment. For the extortion treatments (a,b), these circles are below the diagonal (that is, extortioners outcompete their human co-players), whereas for the generosity treatments (c,d) these circles are above the diagonal (that is, generous players let their co-players succeed).

Figure 3. Human cooperation rates over the course of the game.

The graph shows the fraction of cooperating human subjects for each round for the two generosity treatments and the two extortion treatments. Dots represent the outcome of the experiment, with the shaded areas depicting the 95% confidence interval. Both curves start with cooperation rates around 30–40%. However, for the generous strategies we find a significant trend towards more cooperation, whereas for the extortionate strategies the average cooperation rates remain stable.

Figure 4. Withholding cooperation as a form of costly punishment.

The graph shows the effects of of human cooperation on the payoffs of ZD strategies (a,b) and on the human subjects’ payoffs (c,d). The horizontal axis shows the fraction of rounds in which the human players cooperated. Coloured dots represent the outcome of the experiment, whereas the dashed line depicts the linear regression curve based on a least squares analysis. Human cooperation had a strongly positive impact on the co-player’s payoff, and a weakly positive impact on the own payoff. Thus withholding cooperation punishes extortion.