Complete steady-state rate equation for DNA ligase and its use for measuring product kinetic parameters of NAD⁺-dependent DNA ligase from Haemophilus influenzae

Abstract

Background: DNA ligase seals the nicks in the phosphodiester backbone between Okazaki fragments during DNA replication. DNA ligase has an unusual Bi Ter Ping Pong kinetic mechanism. Its substrates in eubacteria are NAD+ and nicked DNA (nDNA). Its products are nicotinamide mononucleotide (NMN), adenosine 5'-monophosphate (AMP), and sealed DNA. Investigation of the kinetic mechanism and measurement of the kinetic constants of DNA ligase using steady-state kinetics would benefit from the availability of the complete steady-state rate equation, including terms for product concentrations and product-related kinetic constants, which has not previously been published.

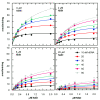
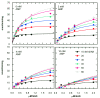
Results: The rate equations for two possible Bi Ter kinetic mechanisms for DNA ligase, including products, are reported. The mechanisms differ according to whether the last two products, AMP and sealed DNA, are released in an ordered or rapid-equilibrium random (RER) manner. Steady-state kinetic studies of product inhibition by NMN and AMP were performed with Haemophilus influenzae NAD+-dependent DNA ligase. The complete rate equation enabled measurement of dissociation constants for NAD+, NMN, and AMP and eliminated one of 3 possible product release mechanisms.

Conclusions: Steady-state kinetic product inhibition experiments and complete steady-state kinetic rate equations were used to measure dissociation constants of NAD+, NMN, and AMP and eliminate the possibility that AMP is the second product released in an ordered mechanism. Determining by steady-state kinetics whether the release of sealed DNA and AMP products goes by an ordered (AMP last off) or RER mechanism was shown to require a product inhibition study using sealed DNA.

Figure 1

Two possible Bi Ter Ping Pong Uni-Uni Uni-Bi kinetic mechanisms for DNA ligase. E represents the enzyme with no ligands. EA represents the enzyme with NAD⁺(A) bound. EB represents the substrate-inhibited enzyme with nicked DNA (B) bound. F represents the adenylylated enzyme. FP represents the adenylylated enzyme with NMN (P) bound. FB represents the adenylyated enzyme with nicked DNA bound. EQR represents the enzyme with sealed DNA (Q) and AMP (R) bound. EQ represents the enzyme with sealed DNA bound. ER represents enzyme with AMP bound noncovalently. The mechanism in which the release of sealed DNA and AMP is ordered is shown at the top. The mechanism in which the order of release of sealed DNA and AMP is random is shown at the bottom. Kinetic constants relevant to each binding, dissociation, or catalytic step are shown in italics. Since no substrates bind and no products dissociate after the 2^nd step and before the 3^rd step of the reaction, the two steps are combined into FB↔EQR.

Figure 2

Global non-linear least-squares fit of data from NMN product inhibition of H. influenzae DNA ligase. The data were fit to the Bi Ter Ping Pong Uni-Uni Uni-Bi steady-state rate equation with product P present: V = V_max[A][B]/(K_mB[A] + K_mA[B](1 + [B]/K_I) + [A][B] + (K_iaK_mB/K_ip)[P] + (K_mB/K_ip)[A][P] + {K_iaK_mB/(K_ipK_I)}[B][P]). Each data point represents a single measurement. The 60 nM DNA data at 0 mM AMP were omitted due to poor quality.

Figure 3

Global non-linear least-squares fit of data from AMP product inhibition of H. influenzae DNA ligase. The data were fit to the Bi Ter Ping Pong Uni-Uni Uni-Bi steady-state rate equation with product R present: V = V_max[A][B]/(K_mB[A] + K_mA[B](1 + [B]/K_I + [R]/K_ir) + [A][B]) Each data point represents a single measurement.